The sin of angle difference identity is a trigonometric identity. It’s used to expand sin of subtraction of two angles functions such as $\sin{(A-B)}$, $\sin{(x-y)}$, $\sin{(\alpha-\beta)}$, and so on. You know how to expand sin of difference of two angles and it’s essential to learn how it is derived in mathematical form in trigonometry.
The sine of difference of two angles formula is derived in trigonometry by the geometrical approach. Geometrically, a right triangle is constructed and it contains difference of two angles. Then, the angle difference identity is derived in mathematical form on the basis of this triangle.
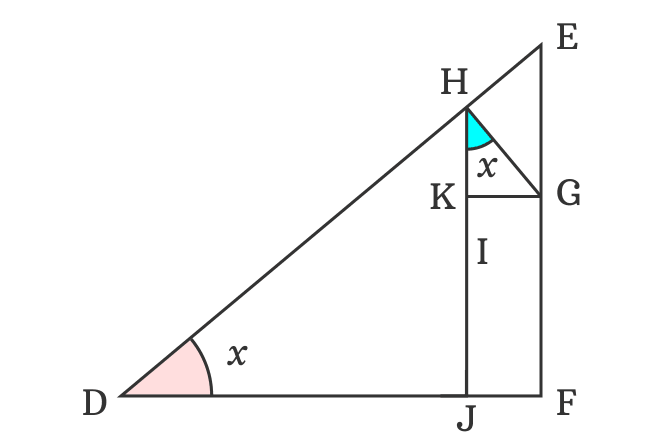
$\Delta EDF$ is a right triangle and the $\angle EDF$ is taken as $x$.
$(1). \,\,\,$ Draw a line from point $D$ to side $\overline{EF}$. It divides the angle $x$ as two angles and intersects the side $\overline{EF}$ at point $G$. If $\angle GDE$ is $y$, then $\angle GDF = x-y$ geometrically.
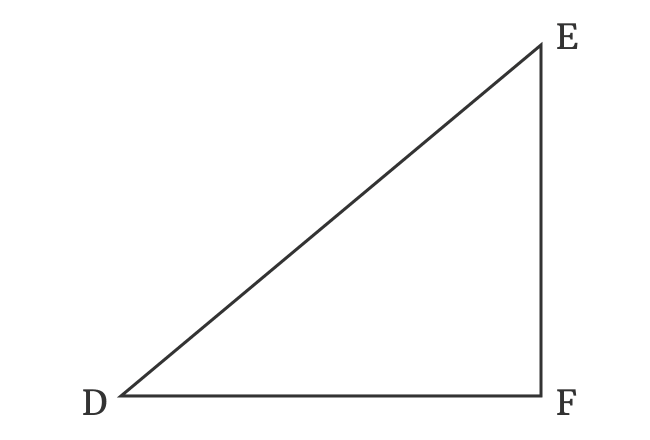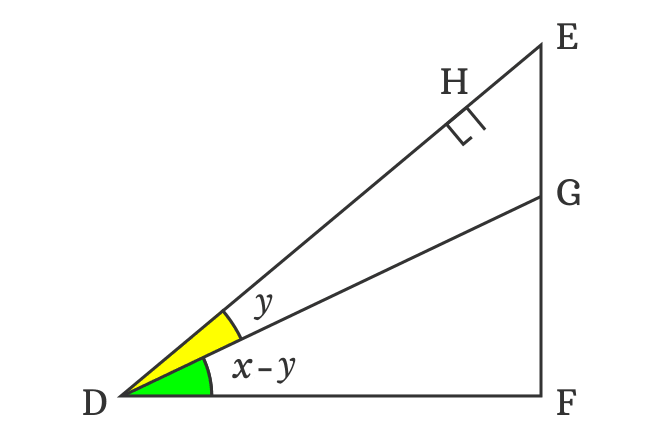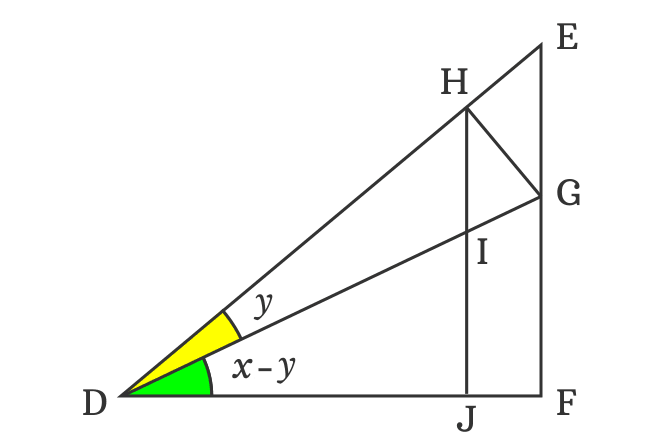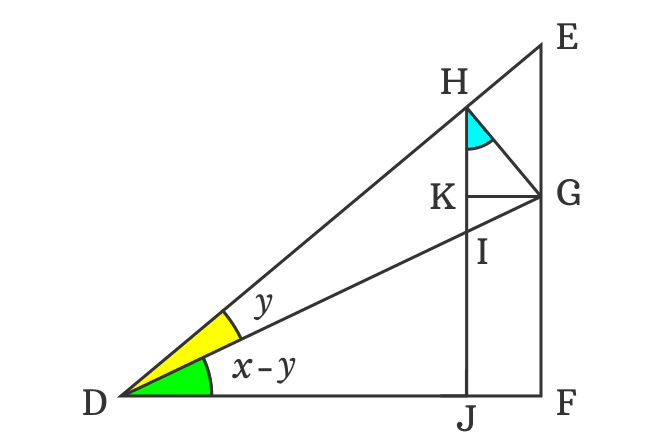
$(2). \,\,\,$ Take set square and draw a perpendicular line to side $\overline{DE}$ but it should intersect the point $G$. Take, the perpendicular intersection point as $H$. In this case, $\overline{DE} \perp \overline{GH}$.
$(3). \,\,\,$ Draw a perpendicular line to side $\overline{DF}$ from $H$ and it intersects the side $\overline{DG}$ at point $I$ and also perpendicularly intersects the side $\overline{DF}$ at point $J$.
$(4). \,\,\,$ Draw a perpendicular line to side $\overline{HJ}$ from point $G$ and it intersects the side $\overline{HJ}$ at point $K$.
The geometrical steps formed three right triangles, and they’re $\Delta GDH$ with angle $y$, $\Delta FDG$ with angle $x-y$ and $\Delta KHG$ with an unknown angle.
In $\Delta GDF$, the $\angle GDF = x-y$. The sine of difference of two angles is written as $\sin{(x-y)}$ and it can be written in its ratio form on the basis of this triangle.
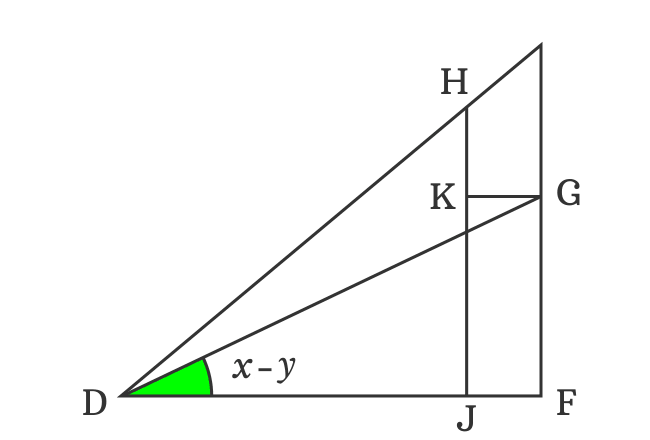
$\sin{(x-y)} \,=\, \dfrac{FG}{DG}$
The sides $\overline{FG}$ and $\overline{KJ}$ are parallel lines and they’re equal. Therefore, $FG = KG$.
$\implies$ $\sin{(x-y)} \,=\, \dfrac{KJ}{DG}$
The perpendicular side $\overline{KG}$ divides the side $\overline{HJ}$ as two sides $\overline{HK}$ and $\overline{KJ}$.
Therefore $HJ = HK+KJ$
$\implies KJ = HJ-HK$
The length of the side $\overline{KJ}$ can be replaced by its equivalent value in the expansion of sin of angle difference function.
$\implies \sin{(x-y)} \,=\, \dfrac{HJ-HK}{DG}$
$\implies \sin{(x-y)} \,=\, \dfrac{HJ}{DG}-\dfrac{HK}{DG}$
$HJ$ is perpendicular of $\Delta HDJ$ and the $\angle HDJ = x$. Try to express $HJ$ in a trigonometric function as per this triangle.
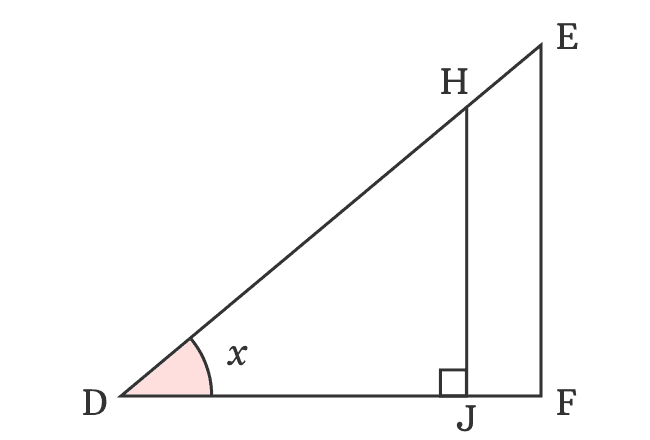
$\sin{x} \,=\, \dfrac{HJ}{DH}$
$\implies$ $HJ \,=\, {DH}\sin{x}$
Now, replace the $HJ$ by its equivalent value in the expansion of $\sin{(x-y)}$ function.
$\implies \sin{(x-y)}$ $\,=\,$ $\dfrac{{DH}\sin{x}}{DG}$ $-$ $\dfrac{HK}{DG}$
$\implies \sin{(x-y)}$ $\,=\,$ $\dfrac{DH}{DG} \times \sin{x}$ $-$ $\dfrac{HK}{DG}$
$DH$ and $DG$ are lengths of adjacent side and hypotenuse in the $\Delta HDG$. The $\angle HDG$ is $y$. Now, express relationship between them in the form of a trigonometric function.
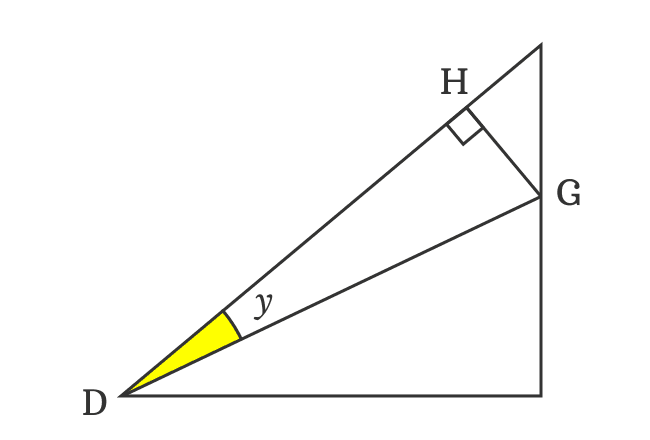
$\cos{y} \,=\, \dfrac{DH}{DG}$
Therefore, the ratio of $DH$ to $DG$ can be replaced by $\cos{y}$ in the expansion of sin of subtraction of two angles function.
$\implies \sin{(x-y)}$ $\,=\,$ $\cos{y} \times \sin{x}$ $-$ $\dfrac{HK}{DG}$
$\implies \sin{(x-y)}$ $\,=\,$ $\cos{y}\sin{x}$ $-$ $\dfrac{HK}{DG}$
$\implies \sin{(x-y)}$ $\,=\,$ $\sin{x}\cos{y}$ $-$ $\dfrac{HK}{DG}$
$HK$ is length of the adjacent side in the $\Delta KHG$ but its angle is unknown and it’s not possible to express $HK$ in the form of a trigonometric function. So, let’s find the $\angle KHG$ geometrically to continue the derivation of sin of angle difference identity.
Two angles are known but an angle is unknown in the $\Delta JDI$. The $\angle JDI = x-y$, $\angle DJI = 90^\circ$ and $\angle DIJ$ is unknown. It can be evaluated by using sum of angles rule of a triangle.
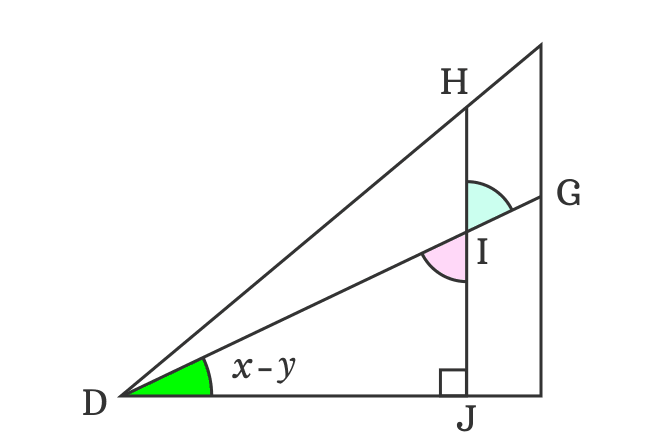
$\angle JDI$ $+$ $\angle DIJ$ $+$ $\angle IJD$ $\,=\,$ $180^\circ$
$\implies$ $x-y$ $+$ $\angle DIJ$ $+$ $90^\circ$ $\,=\,$ $180^\circ$
$\implies$ $\angle DIJ$ $\,=\,$ $180^\circ-90^\circ-x+y$
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle DIJ$ $\,=\,$ $90^\circ-x+y$
The $\angle DIJ$ and $\angle GIH$ are vertically opposite angles. Therefore, they are equal geometrically.
$\angle GIH$ $\,=\,$ $\angle DIJ$
$\,\,\, \therefore \,\,\,\,\,\, \angle GIH$ $\,=\,$ $90^\circ-x+y$
The $\angle DIG$ is a straight angle but it’s divided as two angles $\angle DIH$ and $\angle GIH$ by the intersection of the side $\overline{IH}$.
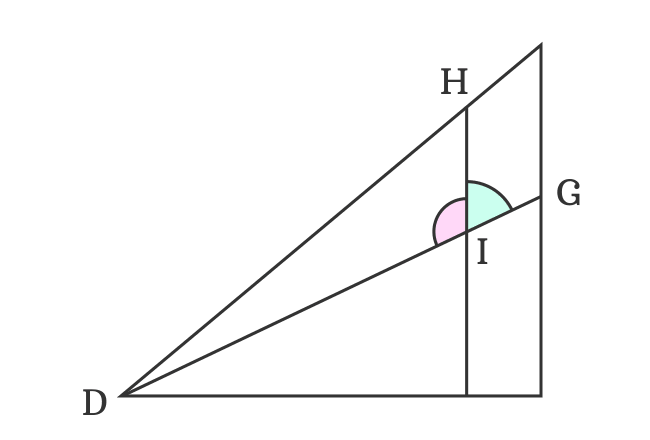
Therefore, $\angle DIG \,=\, 180^\circ$
$\implies$ $\angle DIH$ $+$ $\angle GIH$ $\,=\,$ $180^\circ$
It is already derived that $\angle GIH$ $\,=\,$ $90^\circ-x+y$
$\implies$ $\angle DIH$ $+$ $90^\circ-x+y$ $\,=\,$ $180^\circ$
$\implies$ $\angle DIH$ $\,=\,$ $180^\circ-90^\circ+x-y$
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle DIH$ $\,=\,$ $90^\circ+x-y$
Therefore, it’s derived that $\angle DIH$ is equal to $90^\circ+x-y$ but it’s one of the angles of the $\Delta IDH$.
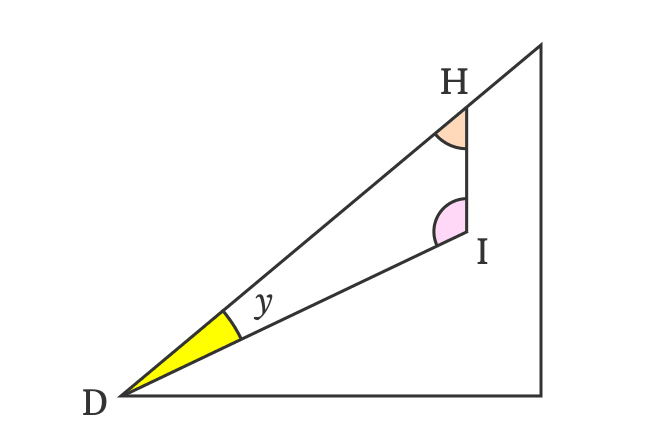
In $\Delta IDH$, the $\angle HDI = y$, $\angle DIH$ $\,=\,$ $90^\circ+x-y$ but $\angle IHD$ is unknown. It can be derived by using sum of angles of a triangle formula.
$\angle DIH$ $+$ $\angle IHD$ $+$ $\angle HDI$ $\,=\,$ $180^\circ$
$\implies$ $90^\circ+x-y$ $+$ $\angle IHD$ $+$ $y$ $\,=\,$ $180^\circ$
$\implies$ $\angle IHD$ $+$ $90^\circ+x-y+y$ $\,=\,$ $180^\circ$
$\implies$ $\angle IHD$ $+$ $\require{cancel} 90^\circ+x-\cancel{y}+\cancel{y}$ $\,=\,$ $180^\circ$
$\implies$ $\angle IHD$ $\,=\,$ $180^\circ-90^\circ-x$
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle IHD$ $\,=\,$ $90^\circ-x$
Actually, the sides $\overline{DH}$ and $\overline{HG}$ are perpendicular lines. So, the angle between them is a right angle.
Therefore, $\angle GHD$ $\,=\,$ $90^\circ$
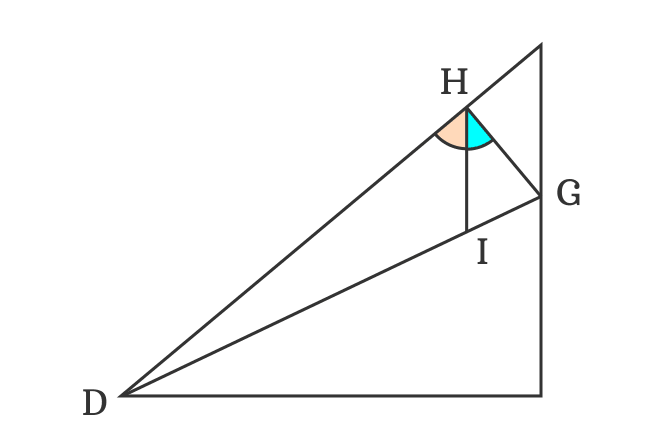
The side $\overline{IH}$ divides the right angle ($\angle GHD$) as two angles $\angle IHD$ and $\angle IHG$ but the $\angle IHD$ is derived as $90^\circ-x$.
$\implies$ $\angle IHD$ $+$ $\angle IHG$ $\,=\,$ $90^\circ$
$\implies$ $90^\circ-x$ $+$ $\angle IHG$ $\,=\,$ $90^\circ$
$\implies$ $\angle IHG$ $\,=\,$ $90^\circ-90^\circ+x$
$\implies$ $\angle IHG$ $\,=\,$ $\require{cancel} \cancel{90^\circ}-\cancel{90^\circ}+x$
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle IHG$ $\,=\,$ $x$
The $\angle IHG$ and $\angle KHG$ are congruent angles.
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle KHG = x$
Therefore, it is calculated that the angle of $\Delta KHG$ is $x$. Actually, the angle of $\Delta EDF$ is also $x$. It is possible because the $\Delta EDF$ and $\Delta KHG$ are similar triangles.
The angle of $\Delta KHG$ is known and the proof of $\sin{(x-y)}$ can be continued further.
$\implies \sin{(x-y)}$ $\,=\,$ $\sin{x}\cos{y}$ $-$ $\dfrac{HK}{DG}$
The $HK$ can be expressed in the form a trigonometric function.
$\cos{x} \,=\, \dfrac{HK}{HG}$
$\implies$ $HK \,=\, {HG}\cos{x}$
$\implies \sin{(x-y)}$ $\,=\,$ $\sin{x}\cos{y}$ $-$ $\dfrac{{HG}\cos{x}}{DG}$
$\implies \sin{(x-y)}$ $\,=\,$ $\sin{x}\cos{y}$ $-$ $\dfrac{HG}{DG} \times \cos{x}$
$HG$ and $DG$ are lengths of the opposite side and hypotenuse in the $\Delta HDG$. The angle of this triangle is $y$. The relationship of angle with the ratio between them can expressed in the form of a trigonometric function.

$\sin{y} \,=\, \dfrac{HG}{DG}$
Now, substitute the ratio of $HG$ to $DG$ by its equivalent value in the expansion of sine of difference of two angles.
$\implies \sin{(x-y)}$ $\,=\,$ $\sin{x}\cos{y}$ $-$ $\sin{y} \times \cos{x}$
$\implies \sin{(x-y)}$ $\,=\,$ $\sin{x}\cos{y}$ $-$ $\sin{y}\cos{x}$
$\,\,\, \therefore \,\,\,\,\,\,$ $\sin{(x-y)}$ $\,=\,$ $\sin{x}\cos{y}$ $-$ $\cos{x}\sin{y}$
Therefore, it is proved that sine of difference of two angles is equal to subtraction of products of sin and cosine of the two angles.
It is called sin of angle difference identity or sin of subtraction of two angles and used as a formula in mathematics.
The sin of angle difference identity can also be written in several ways.
For example, if $A$ and $B$ are angles, then the sin of subtraction of two angles is $\sin{(A-B)}$ but it is expanded in the same form.
$(1) \,\,\,$ $\sin{(A-B)}$ $\,=\,$ $\sin{A}\cos{B}$ $-$ $\cos{A}\sin{B}$
Similarly, if $\alpha$ and $\beta$ are two angles, then the sine of difference of two angles is written as $\sin{(\alpha-\beta)}$ and it is expanded as follows.
$(2) \,\,\,$ $\sin{(\alpha-\beta)}$ $\,=\,$ $\sin{\alpha}\cos{\beta}$ $-$ $\cos{\alpha}\sin{\beta}$
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved