Vertically opposite angles

The opposite angles which have a common vertex are called the vertically opposite angles.

Introduction

According to English language, the noun of vertical is a vertex or zenith, and we’re not considering the meaning of vertical as perpendicular to something in this case.

Now, let’s discuss about it to understand the concept of vertically opposite angles geometrically.

When two straight lines are intersected at a point, four angles are formed geometrically at the point of their intersection. The point of intersection is a common vertex to each angle. In this case, the vertex is called as a vertical.

There are two pairs of opposite angles in the point of view of the vertical. Each pair of opposite angles in the point of vertical is called the vertically opposite angles and they are equal geometrically.

Example

$\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ are two straight lines, which are intersected at point $O$ and four angles are formed geometrically by their intersection.

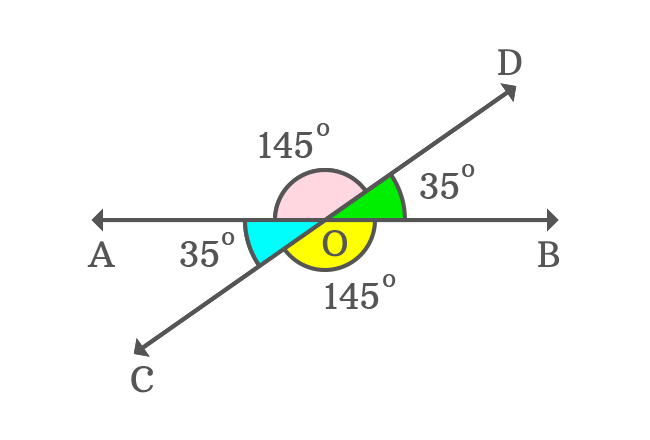
The point of intersection of them is called a vertical in this case and the four angles are measured as.

$(1). \,\,\,$ $\angle BOD$ $\,=\,$ $35^°$

$(2). \,\,\,$ $\angle DOA$ $\,=\,$ $145^°$

$(3). \,\,\,$ $\angle AOC$ $\,=\,$ $35^°$

$(4). \,\,\,$ $\angle COB$ $\,=\,$ $145^°$

In the point of view of vertical ($O$), the angles $\angle BOD$ and $\angle AOC$ are opposite to each other. So, they’re called as vertically opposite angles.

Similarly, the angles $\angle DOA$ and $\angle COB$ are also called as vertically opposite angles. Thus, the vertically opposite angles are formed geometrically.

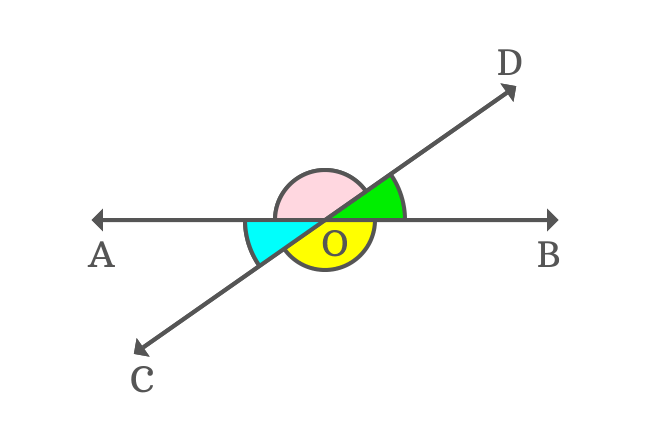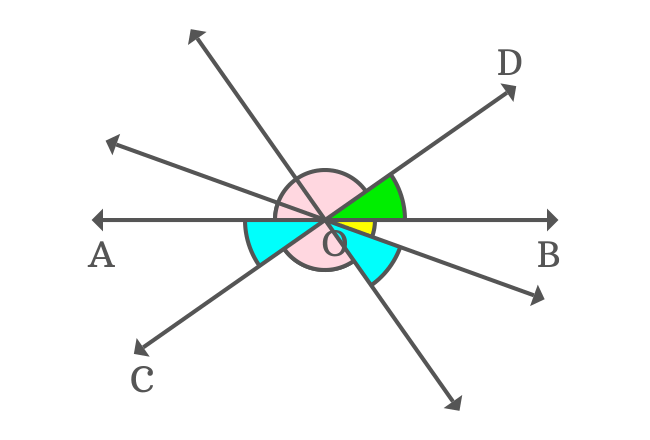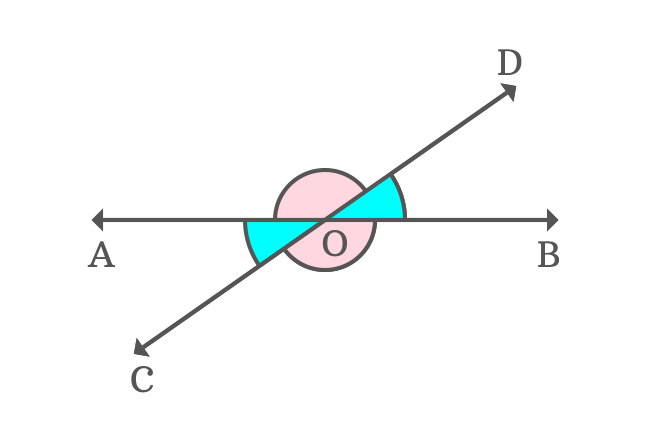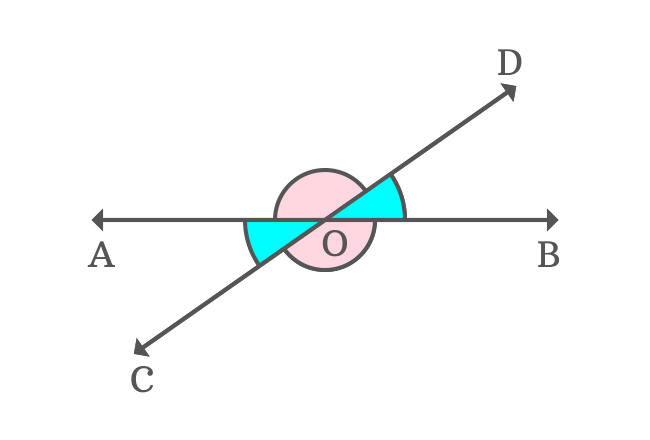
The vertically opposite angles $\angle BOD$ and $\angle AOC$ are equal and each angle is $35^°$. Similarly, the vertically opposite angles $\angle DOA$ and $\angle COB$ are also equal and each angle is $145^°$.

The $\angle DOA$ and $\angle AOC$ are adjacent angles and the sum of them forms a straight angle. Similarly, the $\angle BOD$ and $\angle COB$ are also adjacent angles and the sum of them is also equal to $180^°$.

If one pair of adjacent angles are rotated by $180^°$, they are exactly same as the other pair of adjacent angles.

It makes one pair of vertically opposite angles becomes other pair of vertically opposite angles geometrically. Therefore, the vertically opposite angles are always equal geometrically.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.