An angle that denotes null is called zero angle.
In some cases, the angle between sides of an object or objects is null. So, a geometric concept is required to express that angle and it was introduced as zero angle in geometry. It can also be called as null angle.
There are two notable factors to understand this concept.
The concept of zero angle can be described now by considering the above two natural factors.

The surface of earth on which we walk daily is horizontal. So, a horizontal line can be considered as a line of indicating zero angle but it should start from left and should continue its journey towards right.
The above explanation helps you to have basic knowledge on zero angle and let’s learn its concept further from a graphical example as follows.

Consider a point on the plane and denote it by a letter $\small O$. A line is started from that point. It passed through a point $\small P$ and the ray $\small \overrightarrow{OP}$ is formed geometrically. Similarly, another line is started from point $\small O$. It passed through a point $\small Q$ and the ray $\small \overrightarrow{OQ}$ is formed geometrically.
Now, let’s analyze this geometric figure to know about zero angle clearly.
The rays $\small \overrightarrow{OP}$ and $\small \overrightarrow{OQ}$ both are not parallel to the surface of earth. So, the rays $\small \overrightarrow{OP}$ and $\small \overrightarrow{OQ}$ are not representing zero angle. The rays $\small \overrightarrow{OP}$ and $\small \overrightarrow{OQ}$ have a vertex $\small O$. Therefore, an angle should be formed between them at their meeting point $\small O$ and the angle is written as $\small \angle POQ$ or $\small \angle QOP$ or $\small \angle O$.
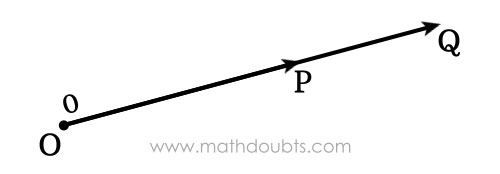
However, the rays $\small \overrightarrow{OP}$ and $\small \overrightarrow{OQ}$ both are in same direction and have a meeting point. So, the angle between the rays $\small \overrightarrow{OP}$ and $\small \overrightarrow{OQ}$ is null, which means the angle between them is zero angle.
$\,\,\,\therefore\,\,\,\,\,\,$ $\small \angle POQ$ $\,=\,$ $\small \angle QOP$ $\,=\,$ $\small \angle O$ $\,=\,$ $0$
There are three methods to express zero angle in mathematics.
The zero angle is written as $0^\circ$ mathematically and it is read as zero degrees.
The zero angle is written as $0^r$ mathematically. It is simply written as $0$ in mathematics and it is read as zero radians.
The zero angle is written as $0^g$ mathematically and it is read as zero gradians.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved