The cot of angle sum identity is an identity in trigonometry, used as formula to expand cot of sum of two angles functions such as $\cot{(A+B)}$, $\cot{(x+y)}$, $\cot{(\alpha+\beta)}$, and so on. You have learned how to expand them and it’s time to know how cot of angle sum identity is derived mathematically in trigonometry.
The cot of sum of two angles formula is originally derived in mathematical form in trigonometry by the geometrical approach. A right triangle with sum of two angles is required to derive this identity.
The $\Delta GFH$ is a right triangle and the angle of this triangle is divided as two angles for expressing cot of sum of two angles in mathematical form.
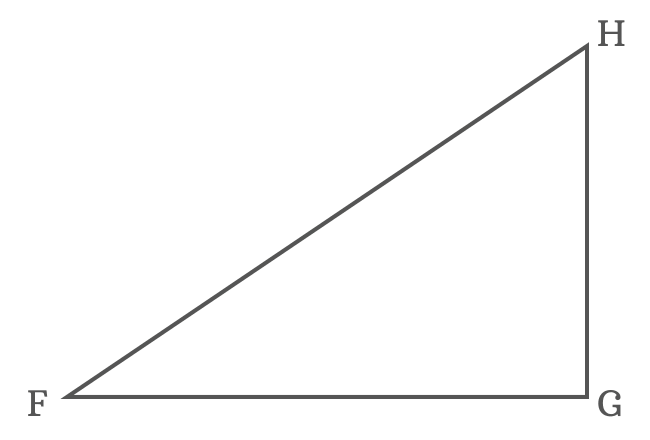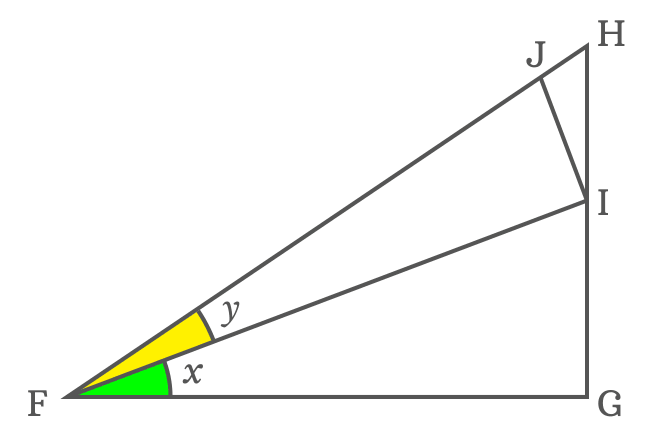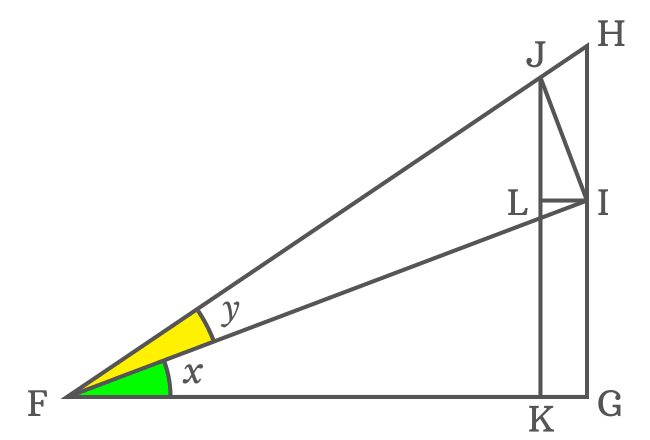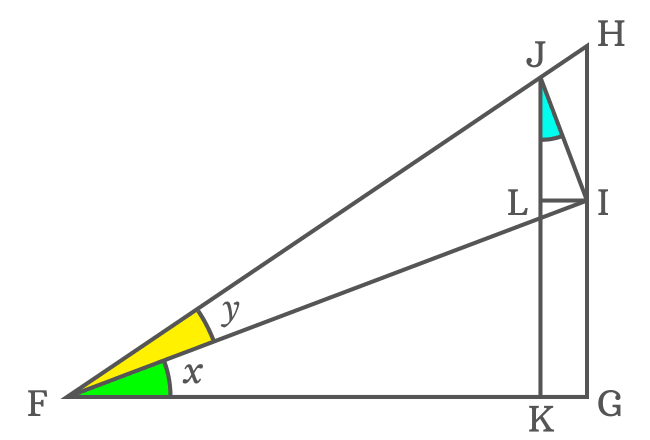
$(1). \,\,\,$ In order to divide $\angle GFH$ as two angles $x$ and $y$, a straight line should be drawn from point $F$ to side $\overline{GH}$ and it intersects the side $\overline{GH}$ at point $I$.
$(2). \,\,\,$ Draw a perpendicular line to side $\overline{FI}$ but it should start from point $I$ and intersect the side $\overline{FH}$ at point $J$. Therefore $\overline{FI} \perp \overline{JI}$
$(3). \,\,\,$ Next, draw a perpendicular line to side $\overline{FG}$ from point $J$ and it perpendicularly intersects the side $\overline{FG}$ at point $K$.
$(4). \,\,\,$ Similarly, draw a perpendicular line to side $\overline{JK}$ from point $I$ and it intersects the side $\overline{JK}$ at point $L$.
The four geometrical steps constructed a right triangle which contains the $\Delta GFI$ with angle $x$, $\Delta IFJ$ with angle $y$ and $\Delta IJL$ with an unknown angle.
The $\angle KFJ = x+y$ in the $\Delta KFJ$. Now, write cotangent of compound angle $x+y$ in its ratio form according to this triangle.
$\cot{(x+y)}$ $\,=\,$ $\dfrac{FK}{JK}$
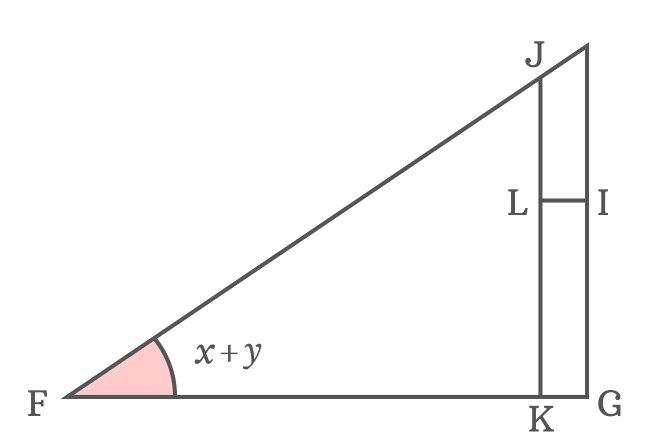
The side $\overline{JK}$ divides the side $\overline{FG}$ as two sides $\overline{FK}$ and $\overline{KG}$.
$FG \,=\, FK+KG$
$\implies FK \,=\, FG\,–\,KG$
In the same way, the side $\overline{IL}$ divides the side $\overline{JK}$ as two sides $\overline{JL}$ and $\overline{LK}$. So, $JK \,=\, JL+LK$.
Now, replace the lengths of the sides $\overline{FK}$ and $\overline{JK}$ by their equivalent values in the $\cot{(x+y)}$ expansion.
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{FG\,–\,KG}{JL+LK}$
The sides $\overline{KG}$ and $\overline{IL}$ are parallel lines. Therefore, $KG = IL$. The sides $\overline{LK}$ and $\overline{IG}$ are also parallel lines. So, $LK = IG$. Now, replace $KG$ by $IL$ and also replace $LK$ by $IG$.
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{FG\,–\,IL}{JL+IG}$
$FG$ is length of the adjacent side in the $\Delta GFI$ and the angle of this triangle is $x$. So, the length of the side $\overline{FG}$ can be written in the form of cot function.
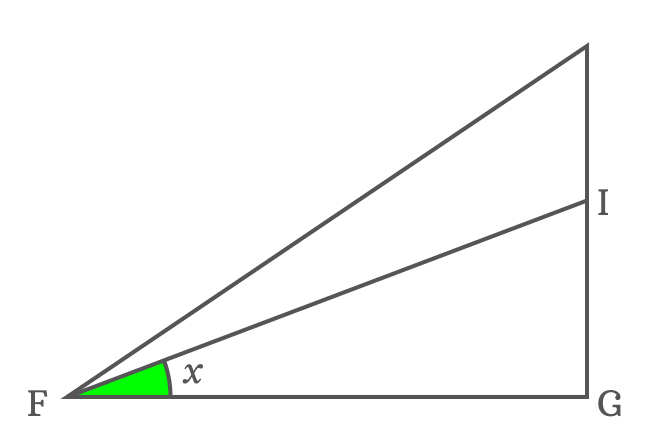
$\cot{x} \,=\, \dfrac{FG}{IG}$
$\implies FG \,=\, {IG}\cot{x}$
The length of the side $\overline{FG}$ can be replaced by its equivalent value in the expansion of cot of sum of two angles identity.
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{{IG}\cot{x}\,–\,IL}{JL+IG}$
$JL$ is the length of the base of the $\Delta LJI$ but its angle is unknown. So, it’s impossible to express the length of the side $\overline{JL}$ in the form of cot function without knowing angle of this triangle. So, let’s find it geometrically.
The sides $\overline{IL}$ and $\overline{FG}$ are parallel lines and $\overline{IF}$ is their transversal. Geometrically, the $\angle LIF$ and $\angle GFI$ are alternate interior angles, and they are equal.
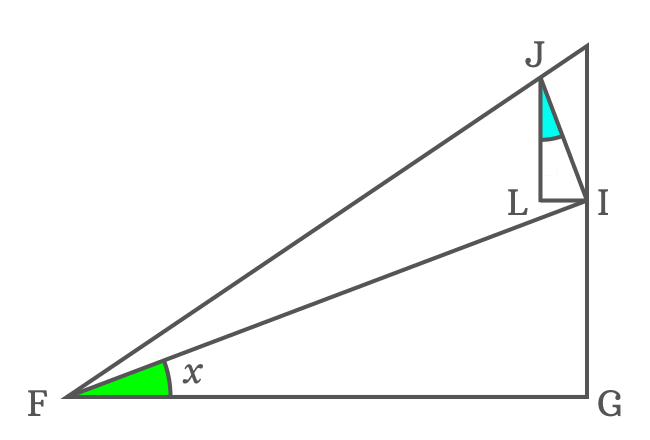
$\angle LIF \,=\, \angle GFI$ but the $\angle GFI = x$
$\therefore \,\,\,\,\,\, \angle LIF \,=\, x$
Geometrically, $\overline{IJ} \perp \overline{FI}$. So, $\angle FIJ = 90^°$. The side $\overline{IL}$ splits the $\angle FIJ$ as two angles $\angle FIL$ and $\angle LIJ$.
$\angle FIJ \,=\, \angle LIF + \angle LIJ$
$\implies 90^° = x+\angle LIJ$
$\,\,\, \therefore \,\,\,\,\,\, \angle LIJ = 90^°-x$
Two angles are known in $\Delta IJL$ and third angle can be calculated by the sum of angles of a triangle formula.
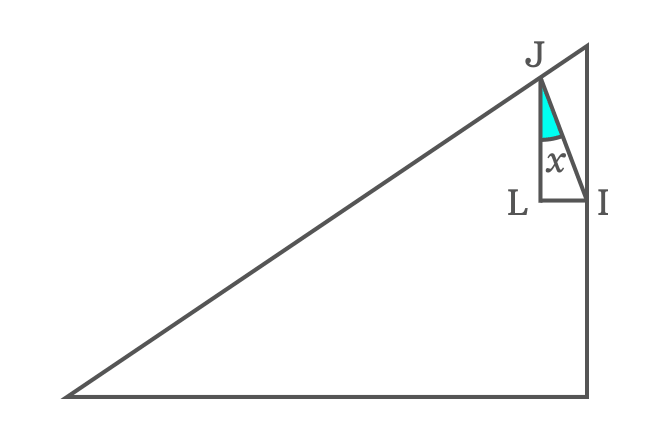
$\angle IJL + \angle JLI + \angle LIJ$ $\,=\,$ $180^°$
$\implies$ $\angle IJL + 90^° + 90^°-x$ $\,=\,$ $180^°$
$\implies$ $\angle IJL + 180^°-x$ $\,=\,$ $180^°$
$\implies$ $\angle IJL$ $\,=\,$ $180^°-180^°+x$
$\implies$ $\angle IJL$ $\,=\,$ $\require{cancel} \cancel{180^°}-\cancel{180^°}+x$
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle IJL \,=\, x$
It is evaluated that $\angle IJL$ is equal to $x$ but $\angle GFI$ is also equal to $x$ and it proves that they both are congruent angles. Similarly, $\Delta GFI$ and $\Delta IJL$ are similar triangles.
Now, let’s continue deriving the expansion of cot of angle sum identity.
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{{IG}\cot{x}\,–\,IL}{JL+IG}$

$JL$ is adjacent side of the $\Delta IJL$ and the angle of this triangle is derived as $x$. Now, express the length of the side $\overline{JL}$ in the form of cot function.
$\cot{x} \,=\, \dfrac{JL}{IL}$
$\implies JL \,=\, {IL}\cot{x}$
It’s time to replace the $JL$ by its equivalent value in the expansion of cot angle sum identity.
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{{IG}\cot{x}\,–\,IL}{{IL}\cot{x}+IG}$
Now, take $IL$ common from both terms in the numerator and denominator. It is useful in simplifying the expansion of $\cot{(x+y)}$ identity.
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{{IL}\Bigg(\dfrac{IG}{IL} \times \cot{x}\,–\,1\Bigg)}{{IL}\Bigg(\cot{x}+\dfrac{IG}{IL}\Bigg)}$
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\require{cancel} \dfrac{\cancel{IL}\Bigg(\dfrac{IG}{IL} \times \cot{x}\,–\,1\Bigg)}{\cancel{IL}\Bigg(\cot{x}+\dfrac{IG}{IL}\Bigg)}$
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{\dfrac{IG}{IL} \times \cot{x}\,–\,1}{\cot{x}+\dfrac{IG}{IL}}$
$IG$ and $IL$ are lengths of opposite sides of the $\Delta GFI$ and $\Delta IJL$. The angles of both triangles are same. Now, find the sine of both triangles.
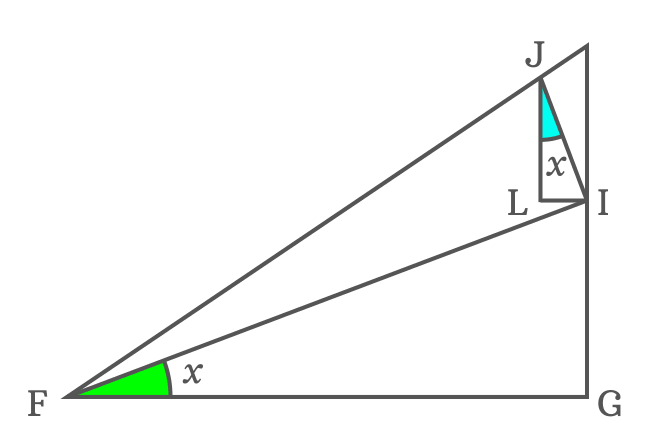
According to $\Delta GFI$, write $\sin{x}$ in its ratio form.
$\sin{x} \,=\, \dfrac{IG}{FI}$
Similarly, write $\sin{x}$ in its ratio form according to $\Delta IJL$
$\sin{x} \,=\, \dfrac{IL}{IJ}$
The ratios are equal because they both are represented by $\sin{x}$.
$\dfrac{IG}{FI}$ $\,=\,$ $\dfrac{IL}{IJ}$
$\implies \dfrac{IG}{IL}$ $\,=\,$ $\dfrac{FI}{IJ}$
Therefore, the quotient of $IG$ by $IL$ can be replaced by the quotient of $FI$ by $IJ$ in the angle sum cot identity’s expansion.
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{\dfrac{FI}{IJ} \times \cot{x}\,–\,1}{\cot{x}+\dfrac{FI}{IJ}}$
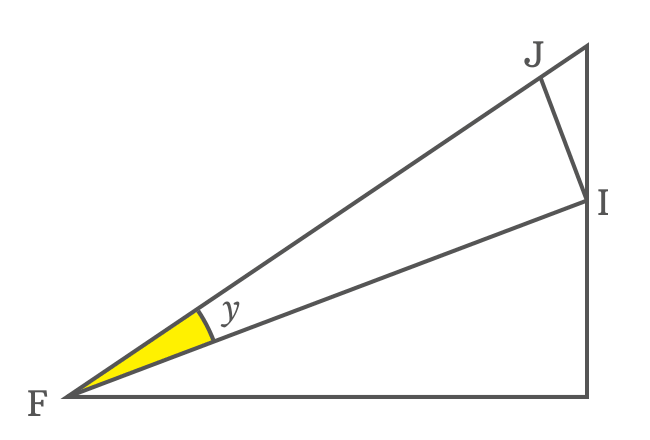
$FI$ and $IJ$ are base and perpendicular of the $\Delta IFJ$, and the angle of this triangle is $y$. The ratio of $FI$ to $IJ$ can be represented by $\cot{y}$ in trigonometry.
$\cot{y} \,=\, \dfrac{FI}{IJ}$
Now, replace the ratio of $FI$ to $IJ$ by $\cot{y}$ in the expansion of cot of compound angle $x+y$.
$\implies$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{\cot{y} \times \cot{x}\,–\,1}{\cot{x}+\cot{y}}$
$\,\,\, \therefore \,\,\,\,\,\,$ $\cot{(x+y)}$ $\,=\,$ $\dfrac{\cot{y}\cot{x}\,–\,1}{\cot{y}+\cot{x}}$
It’s proved that the cot of sum of two angles is equal to the quotient of subtraction of one from product of cotangents of both angles by the sum of the cotangents of the two angles.
The expansion of cot of sum of two angles is called as cot of angle sum identity, and also called as cot of compound angle identity. The cot of angle sum identity is used as a formula in trigonometric mathematics.
The cotangent of angle sum identity can be written in terms of any two symbols. For example, if $A$ and $B$ represent two angles, then the cot of sum of two angles is written as $\cot{(A+B)}$ and it is expanded as follows.
$\cot{(A+B)}$ $\,=\,$ $\dfrac{\cot{B}\cot{A}\,–\,1}{\cot{B}+\cot{A}}$
Similarly, the cot of angle sum formula is written in mathematical form as follows if $\alpha$ and $\beta$ are two angles.
$\cot{(\alpha+\beta)}$ $\,=\,$ $\dfrac{\cot{\beta}\cot{\alpha}\,–\,1}{\cot{\beta}+\cot{\alpha}}$
In this way, the formula for the expansion of cot of angle sum identity is written mathematically in terms of any two angles in trigonometry.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved