Second Quadrant

The left-top side region in the two dimensional space is called the second quadrant.

Introduction

In two dimensional Cartesian coordinate system, two number lines are bisected perpendicularly at their middle point to split the coordinate plane into four equal regions.

The left-top side region is called the second quadrant. Here, the region in the angle $YOX’$ is the second quadrant and denoted by a Roman numeral $II$.

In $\angle YOX’$, the $x$-axis represents negative values and the $y$-axis represents positive values. So, the signs of abscissa and ordinate of each point in this region should be negative and positive respectively.

If $x$-coordinate and $y$-coordinate of each point are represented by $x$ and $y$ respectively, then the values of them are written as $x < 0$ and $y > 0$ in mathematical form.

Usage

The second quadrant in the two dimensional space is used to identity the location of a point whose abscissa is negative and ordinate is positive. Now, let’s learn how to use the second quadrant in coordinate geometry.

Example

Identify the location of the point $B(-5, 2)$.

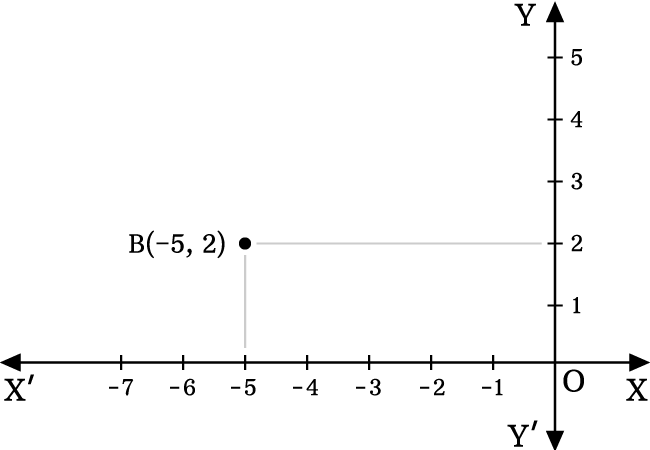
In this example, the $x$ coordinate (or abscissa) is $-5$ and $y$ coordinate (or ordinate) is $2$.

1. Identity $-5$ on negative $x$-axis. Draw a line from $-5$ but the line should be parallel to positive $y$ axis and perpendicular to negative $x$ axis.
2. Identify $2$ on positive $y$ axis. Draw a line from $2$ but the line should be perpendicular to positive $y$ axis and parallel to negative $x$ axis.
3. The two straight lines are intersected perpendicular at a point in the plane and it is called the point $B(-5, 2)$.

In this way, the second quadrant of Bi-dimensional Cartesian coordinate system is used in coordinate geometry for identifying the location of any point whose abscissa is negative and ordinate is positive.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.