Quadrants of Two dimensional space

The region of a coordinate plane that is formed by the perpendicular bisection of two coordinate axes in two dimensional space, is called the quadrant of two dimensional space.

Introduction

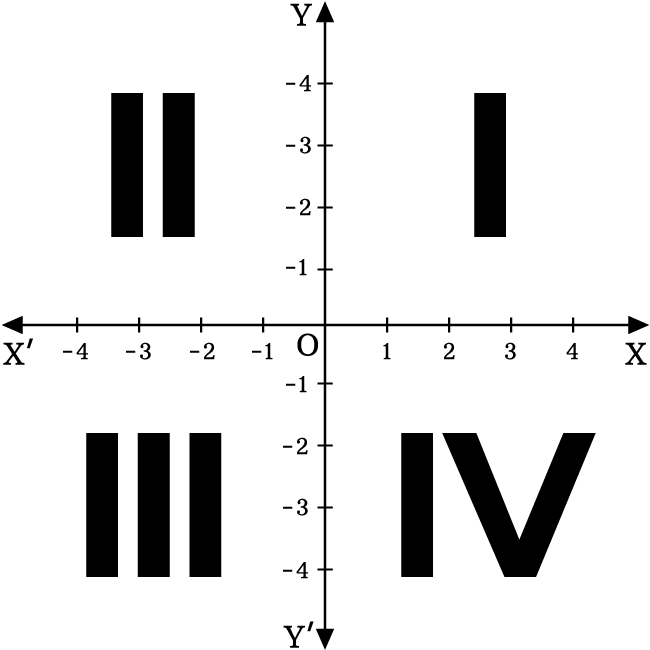
The two dimensional Cartesian coordinate system is actually formed by the perpendicular bisection of two number lines (called as coordinate axes). The perpendicular bisection of coordinate axes split the coordinate plane into four regions. Each region in bi-dimensional space is called the quadrant of two dimensional space.

Quadrants

Every quadrant of the two dimensional Cartesian coordinate system is expressed by a special name.

1. First quadrant
2. Second quadrant
3. Third quadrant
4. Fourth quadrant

Now, let’s learn about every quadrant and its use in two dimensional Cartesian coordinate system with understandable examples.

First Quadrant

The right-top side region in the two dimensional space is called the first quadrant.

It is formed by the perpendicular intersection of the positive $x$ and $y$ axes and it is denoted by a Roman numeral $I$.

In this region, the divisions on the both $x$ and and $y$-axes are represented by positive values. So, signs of the both abscissa and ordinate of each point are positive.

Second Quadrant

The left-top side region in the bi dimensional space is called the second quadrant.

It is formed by the perpendicular intersection of the negative $x$ axis and positive $y$ axis. It is denoted by a Roman numeral $II$.

In this region, the divisions on the $x$ axis and and $y$-axis are represented by negative and positive values. So, the signs of abscissa and ordinate of each point are negative and positive respectively.

Third Quadrant

The left-bottom side region in the two dimensional space is called the third quadrant.

It is formed by the perpendicular intersection of the negative $x$ and $y$ axes and it is denoted by a Roman numeral $III$.

In this region, the divisions on the both $x$ and and $y$-axes are denoted by negative values. So, signs of the both abscissa and ordinate of each point are negative.

Fourth Quadrant

The right-bottom side region in the bi dimensional Cartesian coordinate system is called the fourth quadrant.

It is formed by the perpendicular intersection of the positive $x$ axis and negative $y$ axis. It is represented by a Roman numeral $IV$.

In this region, the divisions on the $x$ axis and and $y$-axis are represented by positive and negative values respectively. So, the signs of abscissa and ordinate of each point are positive and negative respectively.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.