Ordinate

The vertical distance of a point from origin in two dimensional space is called the ordinate. It is also called as the $y$-coordinate.

Introduction

The ordinate is a geometric coordinate of a point, which is helpful to know how far the point is from origin in vertical direction in Bi-dimensional rectangular Cartesian coordinate system.

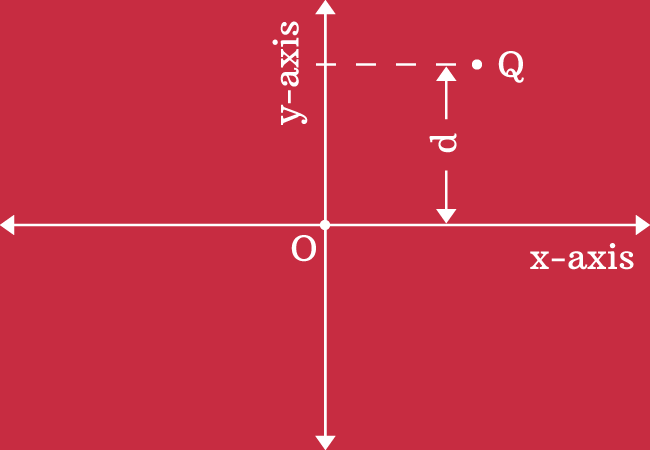
It is measured from origin in vertical direction by comparing the number line on the $y$-axis. Hence, the ordinate is also called as the $y$-coordinate of the point.

The $x$-axis is considered as base line while measuring the ordinate or $y$-coordinate of a point because the $x$-axis is passed through the origin in two dimensional Cartesian coordinate system.

Here, $Q$ is a point on the plane and the vertical distance of the point is measured as $d$ units from origin by taking $x$-axis as base line and also comparing it with the number line on $y$-axis.

Therefore, the vertical distance $d$ is called the ordinate or $y$-coordinate of the point $Q$.

Steps

There are two basic steps to find the ordinate of any point in geometry.

1. From any point, draw a perpendicular line to $y$-axis.
2. The distance from origin to the intersecting point of the perpendicular line on $y$-axis is the ordinate or $y$-coordinate.

Example

Let’s learn how to measure the ordinate or $y$-coordinate of any point from the following understandable example.

Let $P$, $Q$, $R$ and $S$ be four points in a two dimensional rectangular Cartesian coordinate system. Now, use the above two steps to determine the $y$-coordinate of every point.

1. The ordinate of point $P$ is $3$.
2. The $y$-coordinate of point $Q$ is $-4$
3. The ordinate of point $R$ is $1$.
4. The $y$-coordinate of point $S$ is $-2$

Do not forget that the number line on the $y$-axis is considered while measuring the $y$-coordinate. So, it is not required to look at the number line on the $x$-axis.

Thus, the ordinate or $y$-coordinate of every point can be determined geometrically.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.