Non-diagonal elements of a Square Matrix

The elements which do not lie on the leading diagonal of a square matrix is called non-diagonal elements of the matrix.

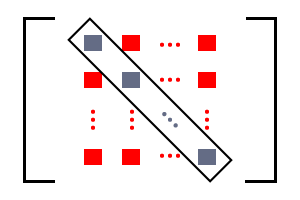
The number of rows is equal to the number of columns in a square matrix. So, a principal diagonal is formed by the first element of first row and last element of last row. The elements which lie on the leading diagonal are known as diagonal elements but the remaining elements in the matrix are known as non-diagonal elements.

$M=\left[\begin{array}{ccccc}{e}_{1\⁣1}& e_{1\⁣2}& e_{1\⁣3}& \cdots & e_{1\⁣n}\\ e_{2\⁣1}& e_{2\⁣2}& e_{2\⁣3}& \cdots & e_{2\⁣n}\\ e_{3\⁣1}& e_{3\⁣2}& e_{3\⁣3}& \cdots & e_{3\⁣n}\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ e_{n\⁣1}& e_{n\⁣2}& e_{n\⁣3}& \cdots & e_{n\⁣n}\end{array}\right]$

$e_{1\⁣1}$ is the first element of first row and $e_{n\⁣n}$ is the last element of last row. They form a leading diagonal on which the elements $e_{2\⁣2},e_{3\⁣3},e_{4\⁣4}$ and etc. also lie.

Except these elements, all remaining elements are non-diagonal elements of the matrix.

Example

$A$ is a square matrix of order $4\times 4$. It is having $16$ elements in four rows and four columns.

$A=\left[\begin{array}{cccc}4& 1& 3& 0\\ –3& 2& 7& 9\\ –5& –8& 4& 6\\ –6& 2& 1& –7\end{array}\right]$

The elements of matrix $A$ is categorized into two types. One type of elements of this matrix is diagonal elements and other type of elements are non-diagonal elements.

The elements $4,2,4$ and $–7$ lie on the leading diagonal but the remaining elements do not lie on the principal diagonal. In other words, $1,3,0,7,9$ and $6$ do not lie on the leading diagonal. Similarly, the elements $–3,–5,–8,–6,2$ and $1$ also do not lie on the principal diagonal.

Therefore, Except $4,2,4$ and $–7$, the elements $1,3,0,7,9,6,–3,–5,–8,–6,2$ and $1$ are non-diagonal elements of the matrix $A$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.