Interior angles of a Triangle

An angle that is formed inside a triangle by the intersection of its sides, is called an interior angle of a triangle.

Introduction

A triangle is formed by connecting the endpoints of three line segments as a closed geometric shape. The intersection of every two sides of a triangle forms an angle internally. Hence, the angle is called an interior angle of triangle. It is also called as an internal angle of a triangle.

In a triangle, the three line segments are intersected at three locations on a plane. Hence, three interior or internal angles are formed inside a triangle.

Example

For understanding the concept of internal angles of a triangle, let’s construct a triangle geometrically.

1. Take three line segments of any length.
2. Form a closed geometric shape by connecting an endpoint of a line segment to an endpoint of another line segment. Thus, a triangle is formed geometrically.
3. The connection of every two line segments inside a triangle forms an angle. The angle is called an interior or internal angle. There are three interior angles formed in a triangle.

Thus, a triangle, denoted by $\Delta MLN$ is formed geometrically.

In this triangle, $\angle LMN$, $\angle MLN$ and $LNM$ are called interior or internal angles of the triangle.

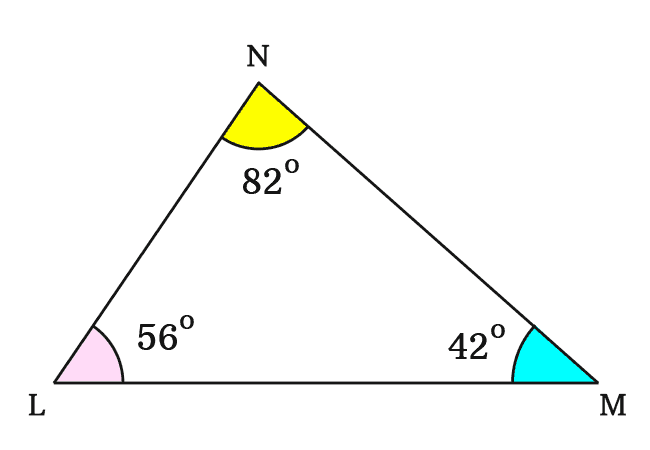
In this example, the internal angles $\angle LMN$, $\angle MLN$ and $LNM$ are unknown but they can be measured by a protractor.

The interior angles in $\Delta MLN$ are measured that

$(1).\,\,\,$ $LMN \,=\, 42^°$

$(2).\,\,\,$ $MLN \,=\, 56^°$

$(3).\,\,\,$ $LNM \,=\, 82^°$

Geometrically, the sum of interior angles in a triangle is equal to $180^°$.

Copyright © 2012 - 2022 Math Doubts, All Rights Reserved