Exterior Angles of a Triangle

An angle between a side and an extended adjacent side of a triangle is called an exterior angle of a triangle.

Introduction

Not only interior angles, the external angles are also formed in triangle.

A side can be extended straightly at any vertex of a triangle. The extended side and its adjacent side forms an angle externally at same vertex of that triangle. The angle made by them is called an exterior angle of the triangle. It is also called as an external angle of the triangle.

In a triangle, two sides can be extended straightly at a vertex. So, two exterior angles are formed at every vertex in a triangle. Therefore, six external angles are possibly formed in a triangle by extending three sides at three vertices in six directions straightly.

Example

$\Delta EFG$ is a triangle on a plane.

Firstly, let’s learn the exterior angles formed at vertex $F$ by extending the sides $\overline{EF}$ and $\overline{FG}$.

∠ GFH

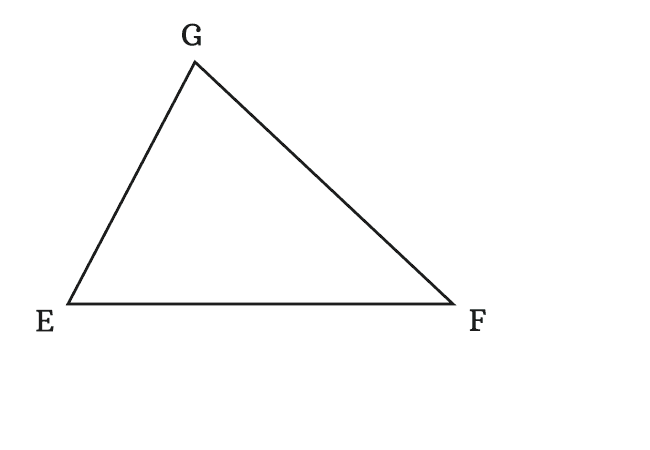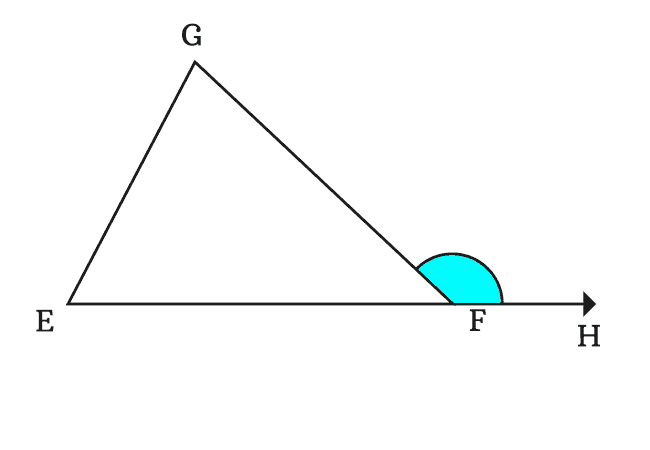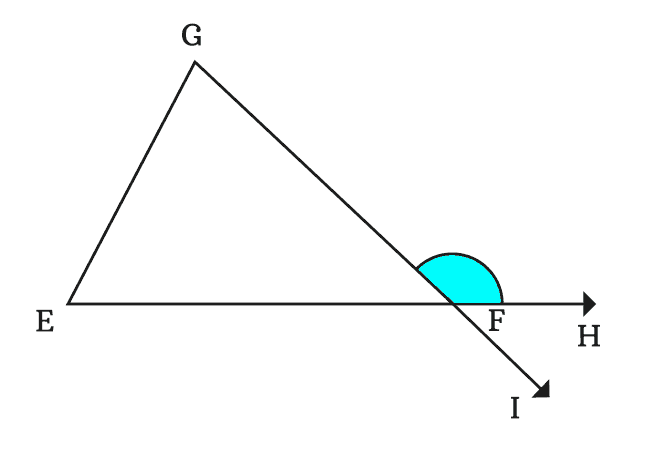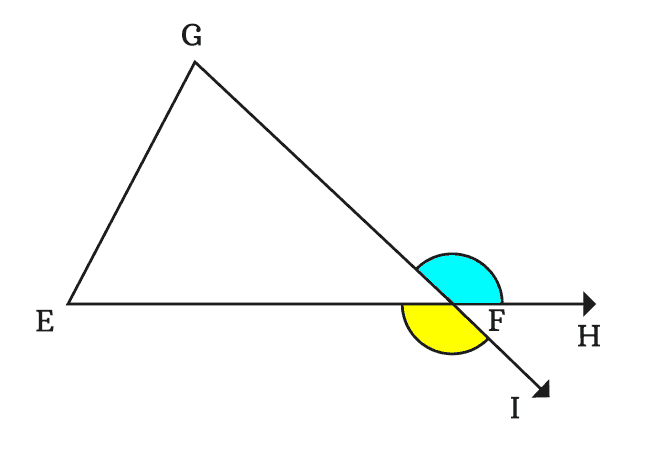
The extension of the side $\overline{EF}$ forms an external angle at vertex $F$ with its adjacent side $\overline{FG}$ when the side $\overline{EF}$ is extended through a point $H$ straightly.

∠ EFI

The extension of the side $\overline{GF}$ forms an exterior angle at vertex $F$ with its adjacent side $\overline{EF}$ when the side $\overline{GF}$ is extended straightly through a point $I$.

Thus, the sides $\overline{EF}$ and $\overline{GF}$ formed two exterior angles $\angle GFH$ and $\angle EFI$ respectively at vertex $F$.

In the same way, let’s draw the external angles formed at vertex $G$ by extending the sides $\overline{FG}$ and $\overline{EG}$.

∠ EGJ

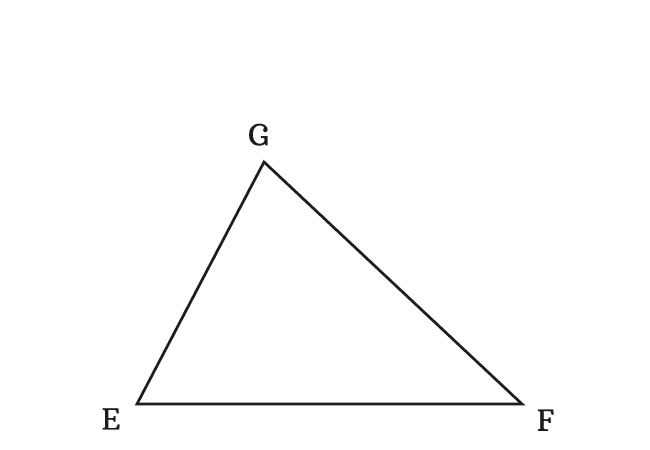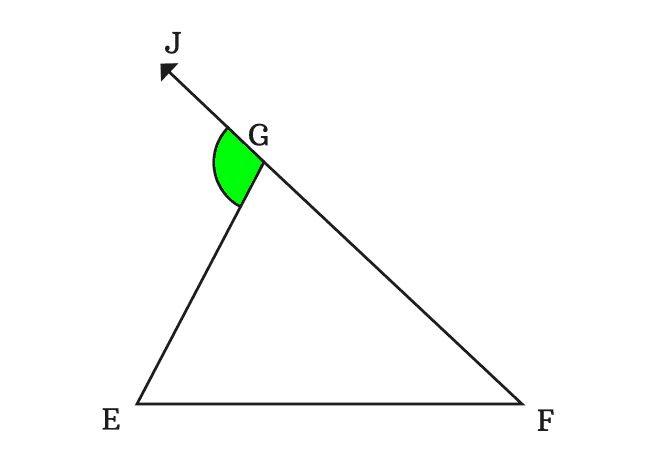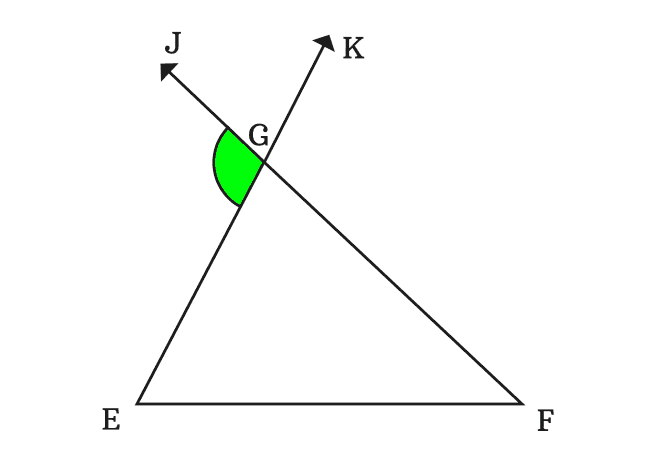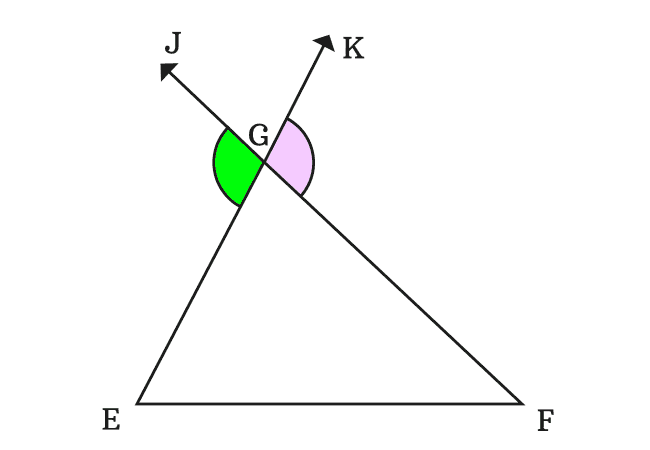
The straight extension of the side $\overline{FG}$ forms an angle externally at vertex $G$ with its adjacent side $\overline{EG}$ when the side $\overline{FG}$ is extended through a point $J$ straightly.

∠ FGK

Similarly, the straight extension of the side $\overline{EG}$ forms an exterior angle at vertex $G$ with its adjacent side $\overline{FG}$ when the side $\overline{EG}$ is extended straightly through a point $K$.

In this way, the sides $\overline{EG}$ and $\overline{FG}$ formed two external angles $\angle EGJ$ and $\angle FGK$ respectively at vertex $G$.

Finally, let’s understand the formation of the exterior angles at vertex $E$ by extending the sides $\overline{FE}$ and $\overline{GE}$.

∠ GEL

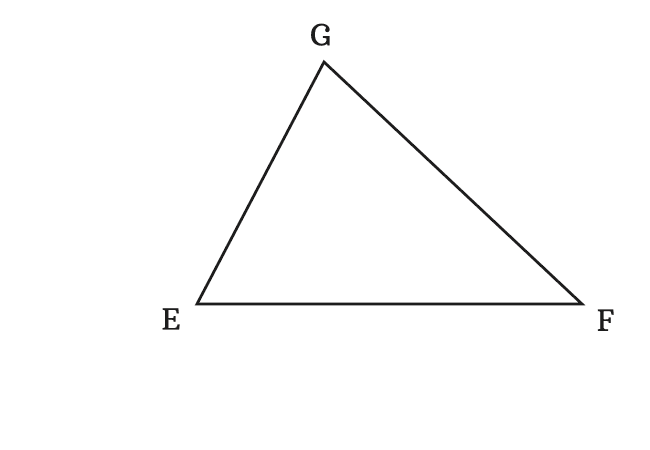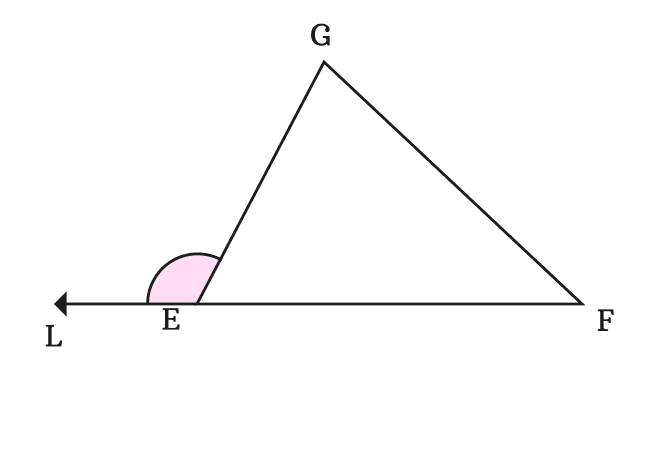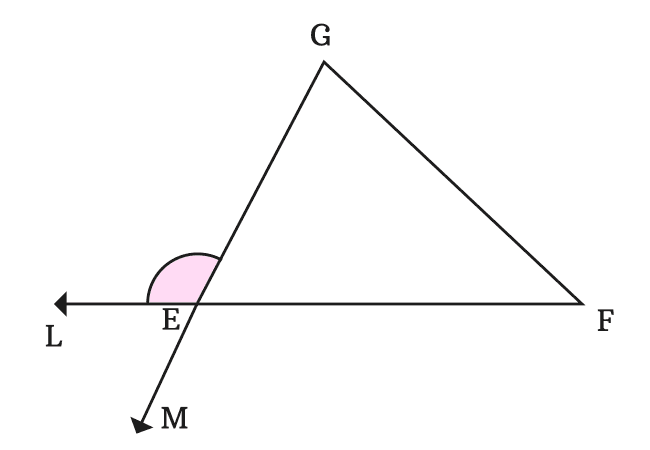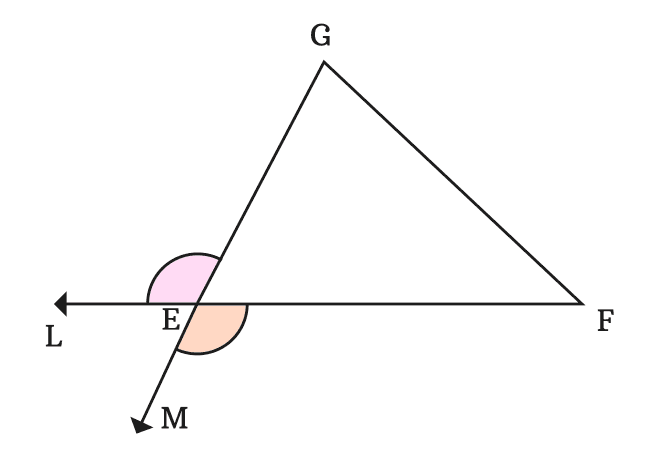
The extension of the side $\overline{FE}$ forms an exterior angle at vertex $E$ with its adjacent side $\overline{GE}$ when the side $\overline{FE}$ is extended straightly through a point $L$.

∠ FEM

The straight extension of the side $\overline{GE}$ forms an exterior angle at vertex $E$ with its adjacent side $\overline{FE}$ when the side $\overline{GE}$ is extended straightly through a point $M$.

Thus, the sides $\overline{FE}$ and $\overline{GE}$ formed two exterior angles $\angle GEL$ and $\angle FEM$ respectively at vertex $E$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.