Evaluate $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{1-\cos{2x}}}{x}}$
The square root of one minus cosine of two times $x$ over $x$ is an irrational function in rational form, whereas $x$ is an algebraic function but it denotes an angle of right triangle and $\cos{2x}$ is a trigonometric function with double angle. The combination of both algebraic and trigonometric form functions formed a special function mathematically.

It is a tough and most important limit problem in calculus and you should be fundamentally strong to understand its solution. However, let’s learn how to find the limit of square root of $1$ minus $\cos{2x}$ divided by $x$ as $x$ approaches to zero from understandable visual explanation.
Evaluate the Limit by Direct Substitution
Firstly, let’s find the limit of the square root of one minus cosine of $2x$ over $x$ as the value of $x$ tends to zero by using the direct substitution method.
$=\,\,$ $\dfrac{\sqrt{1-\cos{2(0)}}}{0}$
$=\,\,$ $\dfrac{\sqrt{1-\cos{(2 \times 0)}}}{0}$
$=\,\,$ $\dfrac{\sqrt{1-\cos{(0)}}}{0}$
$=\,\,$ $\dfrac{\sqrt{1-\cos{0}}}{0}$
According to the trigonometry, the cosine of zero radian is equal to one.
$=\,\,$ $\dfrac{\sqrt{1-1}}{0}$
$=\,\,$ $\dfrac{\sqrt{0}}{0}$
$=\,\,$ $\dfrac{0}{0}$
It is an indeterminate form and it clears that the limit cannot be evaluated by the direct substitution. So, we should find the limit of the given rational function in another method.
Let’s think for simplifying the function before finding its limit. There is a cosine function with double angle in numerator and it can be expanded in terms of sine by using cos double angle identity. It helps us to simplify the given rational function in irrational form.
Try possibility of simplifying the function
Let’s use the cos double angle identity to expand the $\cos{2x}$ function in terms of sine.
$\implies$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{1-\cos{2x}}}{x}}$ $\,=\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{1-(1-2\sin^2{x})}}{x}}$
Now, let’s focus on simplifying the function in the numerator for simplifying the whole irrational function to maximum level.
$=\,\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{1-1+2\sin^2{x}}}{x}}$
$=\,\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{\cancel{1}-\cancel{1}+2\sin^2{x}}}{x}}$
$=\,\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{2\sin^2{x}}}{x}}$
$=\,\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{2 \times \sin^2{x}}}{x}}$
$=\,\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{2} \times \sqrt{\sin^2{x}}}{x}}$
The square root of $2$ is a constant and it can be taken out from the limit operation. So, let’s use the concept of multiplication of fractions to separate $\sqrt{2}$ from rational expression.
$=\,\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{2} \times \sqrt{\sin^2{x}}}{1 \times x}}$
$=\,\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \bigg(\dfrac{\sqrt{2}}{1} \times \dfrac{\sqrt{\sin^2{x}}}{x}\bigg)}$
$=\,\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \bigg(\sqrt{2} \times \dfrac{\sqrt{\sin^2{x}}}{x}\bigg)}$
Now, use the constant multiple limit formula to exclude the irrational constant $\sqrt{2}$ from limit operation.
$=\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{\sin^2{x}}}{x}}$
Look at the function in numerator, where the sine function is in square form and it has square root too. Mathematically, the square root of $\sin^2{x}$ can be simply written as $\sin{x}$ but we should consider its functionality for both negative and positive angles.
Analyzing the function for further simplification
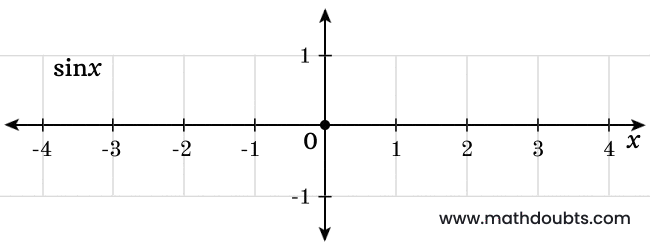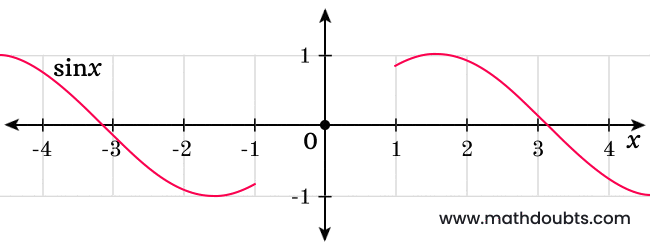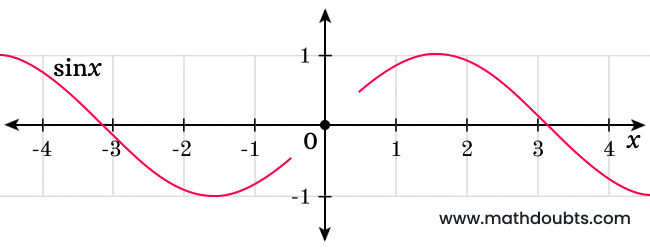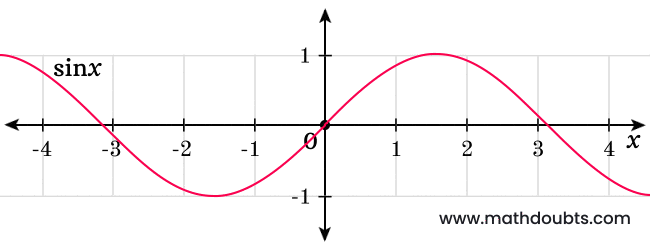
The above visual image expresses sine function’s graph and let’s analyze it when the angle approaches to zero.
- Look at left-side of graph, the sine function’s value is positive or negative for negative angles.
- Look at right-side of graph, the sine function’s value is also positive or negative for positive angles.
It clears that the value of sine function can be either positive or negative and it can be understood clearly from the above sine graph.
Now, let’s study the sine squared function for both positive and negative angles from its graph.
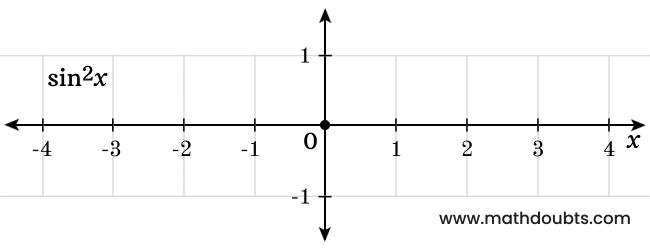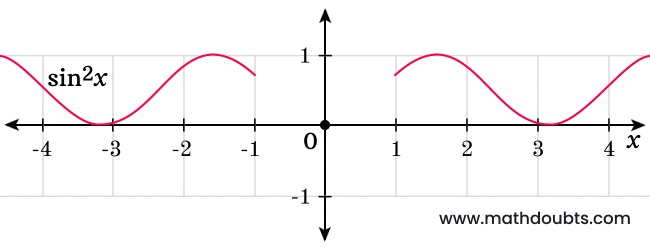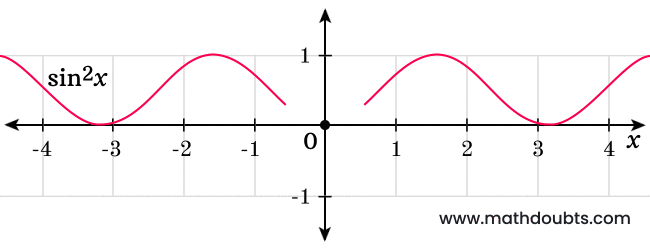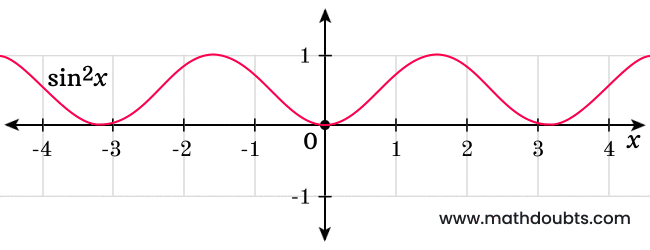
The sine function’s value can be positive or negative but its square is always a positive value for both positive and negative angles. It can be understood from the above sine square function’s graph.
Obviously, the square root of $\sin^2{x}$ is a real number and always a positive value. Now, the square root of sine square of $x$ is an absolute value and it can be written as $|\sin{x}| \ge 0$ in mathematics. So, remember this till the end of solving this hard limit problem.
$\therefore\,\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sqrt{\sin^2{x}}}{x}}$ $\,=\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{|\sin{x}|}{x}}$
The simplification process of given function is completed to maximum level and let’s start the procedure of finding its limit mathematically in calculus.
Evaluating the Limit of the function
Now, let’s find the limit of the function from both left-hand side and right-hand side. The left sided limit and the right sided limit are written mathematically as follows.
$(1).\,\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0^-}{\normalsize \dfrac{|\sin{x}|}{x}}$
$(2).\,\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0^+}{\normalsize \dfrac{|\sin{x}|}{x}}$
Firstly, let’s find the left-sided limit of modulus of $\sin{x}$ over $x$ as the value of $x$ approaches to zero from left. Substitute negative $x$ wherever $x$ in the function to know how the rational function reacts for negative angles.
$\implies$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0^-}{\normalsize \dfrac{|\sin{x}|}{x}}$ $\,=\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{|\sin{(-x)}|}{-x}}$
According to even-odd identity of sine function, the sine of negative angle is equal to negative sine of angle.
$=\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{|-\sin{x}|}{-x}}$
The value of negative $\sin{x}$ can be negative or positive but its absolute value is always positive.
$=\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sin{x}}{-x}}$
Now, let’s focus on further simplifying the function and then we can evaluate the limit. So, once again use the multiplication of fractions concept to break the fractional function as a product of two fractions.
$=\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sin{x}}{-1 \times x}}$
$=\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{1 \times \sin{x}}{-1 \times x}}$
$=\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \bigg(\dfrac{1}{-1} \times \dfrac{\sin{x}}{x}\bigg)}$
$=\,\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \bigg((-1) \times \dfrac{\sin{x}}{x}\bigg)}$
Once again, use the constant multiple rule of limits to release the negative one from the limit operation.
$=\,\,$ $\sqrt{2} \times (-1) \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sin{x}}{x}}$
$=\,\,$ $\big(-\sqrt{2}\big) \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sin{x}}{x}}$
Finally, let’s use the trigonometric limit rule in sine function to find the limit of $\sin{x}$ divided by $x$ as the value of $x$ is closer to zero.
$=\,\,$ $\big(-\sqrt{2}\big) \times 1$
Therefore, it is evaluated that the limit of square root of one minus cosine $2x$ over $x$ as the value of $x$ approaches to zero from left is equal to negative square root of $2$.
$\therefore\,\,\,$ $\displaystyle \large \lim_{x \,\to\, 0^-}{\normalsize \dfrac{\sqrt{1-\cos{2x}}}{x}}$ $\,=\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0^-}{\normalsize \dfrac{|\sin{x}|}{x}}$ $\,=\,$ $-\sqrt{2}$
It can be clearly observed in the following graph of $1$ minus $\cos{2x}$ over $x$ function.
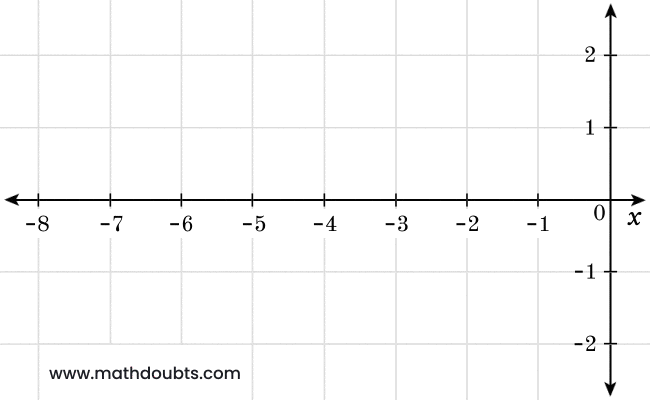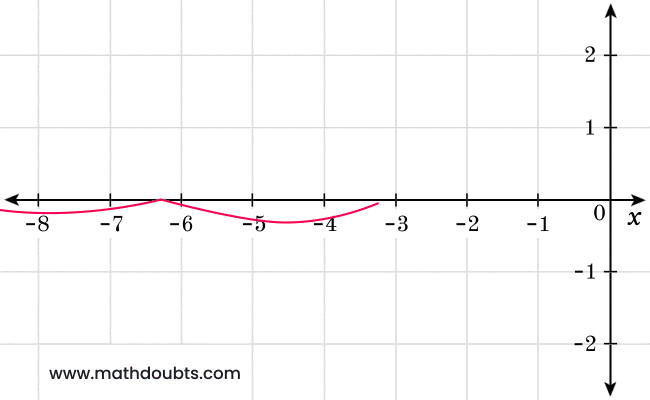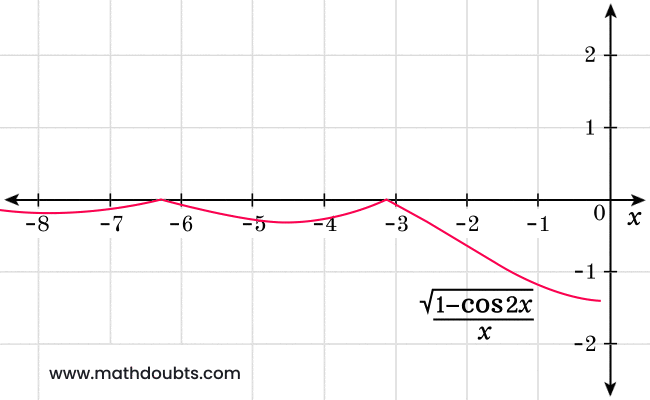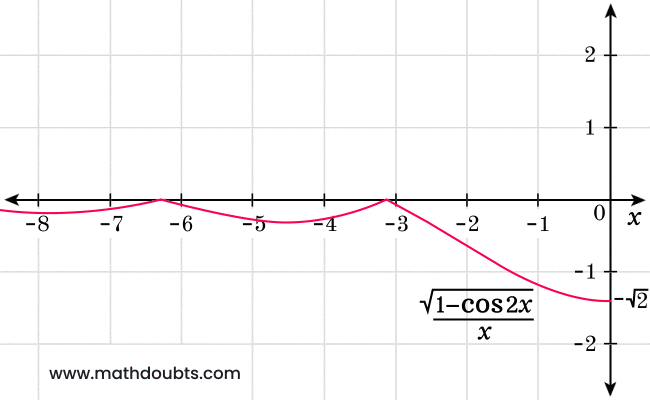
Similarly, let’s find the right-sided limit of $|\sin{x}|$ over $x$ as the value of $x$ approaches to zero. The angles on right side are positive but $\sin{x}$ is negative for even positive angles. However, its modulus is always positive.
When the value of $x$ approaches to $0$ from right side, the sine function is positive and its denominator is also positive. So, the modulus of $\sin{x}$ can be simply written as $\sin{x}$ in this case.
$\implies$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0^+}{\normalsize \dfrac{|\sin{x}|}{x}}$ $\,=\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sin{x}}{x}}$
Now, use the trigonometric limit rule in sine function to find the limit of $\sin{x}$ divided by $x$ as $x$ tends to $0$.
$\implies$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0^+}{\normalsize \dfrac{|\sin{x}|}{x}}$ $\,=\,$ $\sqrt{2} \times 1$
Therefore, it is proved that the limit of square root of $1$ minus $\cos{2x}$ over $x$ as the value of $x$ is closer to $0$ from right side is equal to the square root of $2$.
$\therefore\,\,\,$ $\displaystyle \large \lim_{x \,\to\, 0^+}{\normalsize \dfrac{\sqrt{1-\cos{2x}}}{x}}$ $\,=\,$ $\sqrt{2} \times \displaystyle \large \lim_{x \,\to\, 0^+}{\normalsize \dfrac{|\sin{x}|}{x}}$ $\,=\,$ $\sqrt{2}$
It can also be observed clearly in the below graph of $1$ minus $\cos{2x}$ over $x$ function.
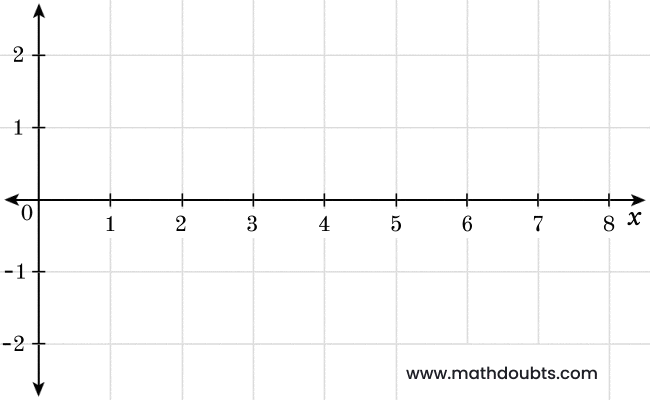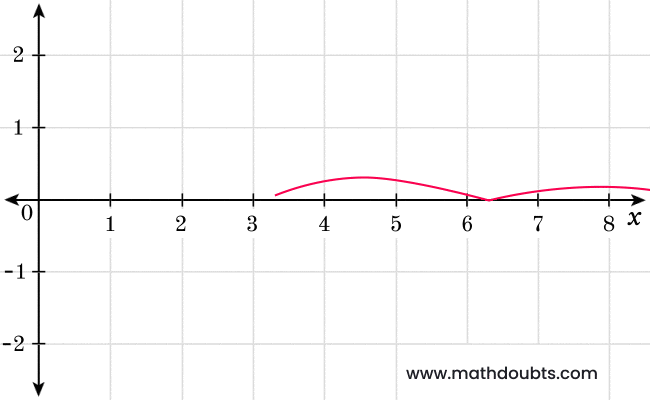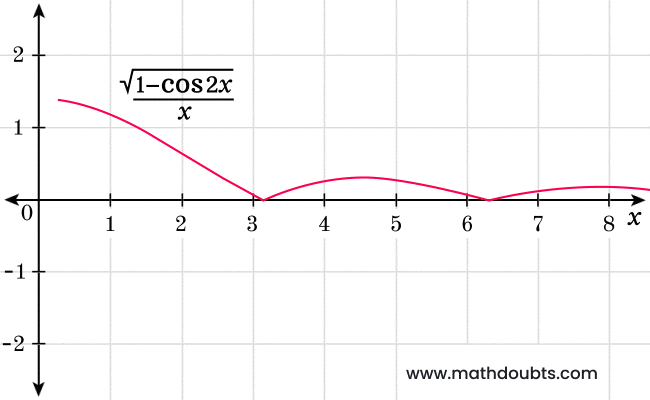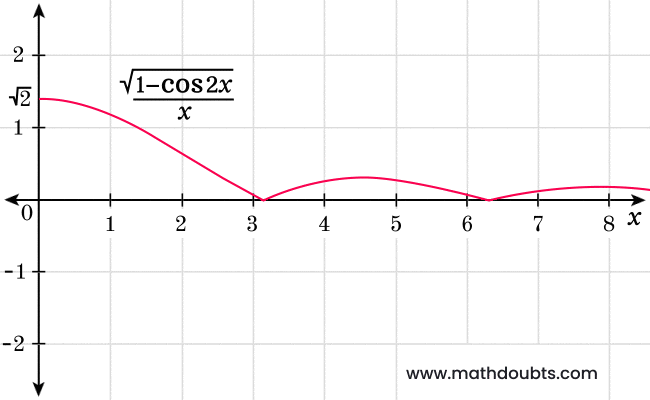
Finally, let’s discuss about the both sided limits of the given function.
$(1).\,\,\,$ $\displaystyle \large \lim_{x \,\to\, 0^-}{\normalsize \dfrac{\sqrt{1-\cos{2x}}}{x}}$ $\,=\,$ $-\sqrt{2}$
$(2).\,\,\,$ $\displaystyle \large \lim_{x \,\to\, 0^+}{\normalsize \dfrac{\sqrt{1-\cos{2x}}}{x}}$ $\,=\,$ $\sqrt{2}$
The left sided limit is not equal to the right sided limit of the square root of $1$ minus $\cos{2x}$ over $x$ as the value of $x$ approaches to zero.
$\displaystyle \large \lim_{x \,\to\, 0^-}{\normalsize \dfrac{\sqrt{1-\cos{2x}}}{x}}$ $\,\ne\,$ $\displaystyle \large \lim_{x \,\to\, 0^+}{\normalsize \dfrac{\sqrt{1-\cos{2x}}}{x}}$
Mathematically, it has proved that the limit of square root of one minus cosine of two times $x$ divided by $x$ does not exist as the value of $x$ approaches to zero.
