Left hand limit

The value of a function as its input approaches some value from left hand side is called the left-hand limit, and also called as the left sided limit.

Introduction

Assume, $x$ is a variable, a function is defined in terms of $x$ and the function is expressed as $f(x)$ simply. Let $a$ represents a constant and $L$ represent the limit of the function $f(x)$.

The left sided limit of the function $f(x)$ is $L$ as the variable $x$ approaches $a$ from left side. In this case, $a^-$ is the closer value of $a$ from left side in Cartesian coordinate system. It can be written in the following mathematical form.

$L \,=\, \displaystyle \large \lim_{x \,\to\, a^-}{\normalsize f(x)}$

Remember, the representation $x \,\to\, a^-$ means it is neither $a$ nor $-a$ but less than $a$ and very closer to $a$.

Example

The concept of left-sided limit can be understood from the following example.

Evaluate $\displaystyle \large \lim_{x \,\to\, 2^-}{\normalsize (x^2-3)}$

In this case, we have to calculate the value of the function $x^2-3$ as the input $x$ closer to $2$ from left-side in the Cartesian coordinate system. According to the two-dimensional space, $0$ and $1$ are near points from left-side of point $2$. So, calculate the values of the function for both values.

1. $f(0) = (0)^2-3 = -3$
2. $f(1) = (1)^2-3 = -2$

But, the point $x = 0$ is two units away from the point $x = 2$ in left-side. Similarly, the point $x = 1$ is one unit away from the point $x = 2$ in left-side. They both are near points but not closer from left-side of the point $x = 2$.

The point $x = 1.9$ is closer point to point $x = 2$ than $x = 0$ and $x = 1$. So, calculate the value of the function.

$f(1.9) = (1.9)^2-3 = 0.61$

There is no doubt about it, the point $x = 1.9$ is closer to point $x = 2$ but the point $x = 2$ is $0.1$ unit away from point $x = 1.9$ and the difference between them is not negligible. Hence, the value of the function $x^2-3$ at point $x = 1.9$ cannot be taken as the limit of the function as $x$ approaches $2$ from left side.

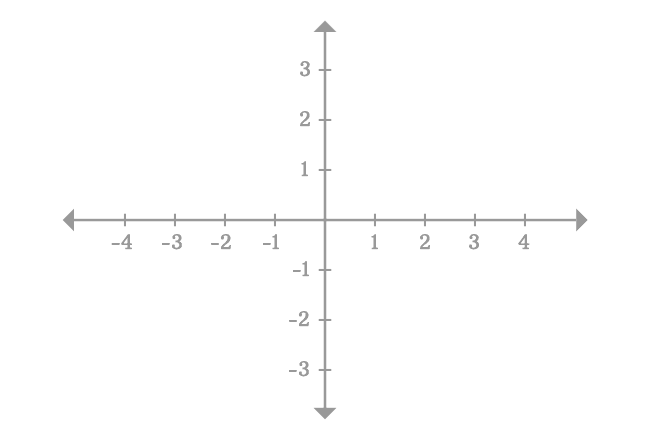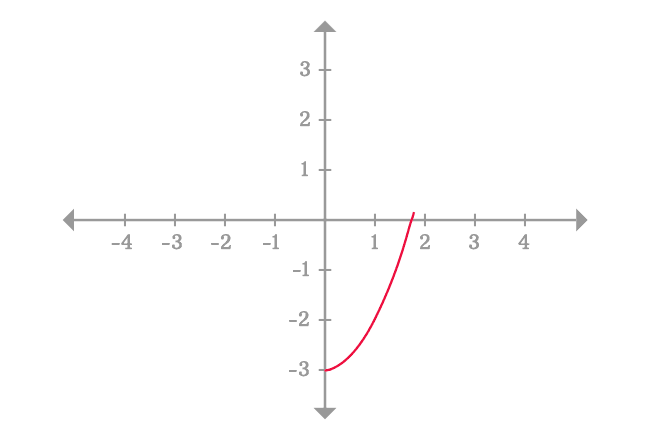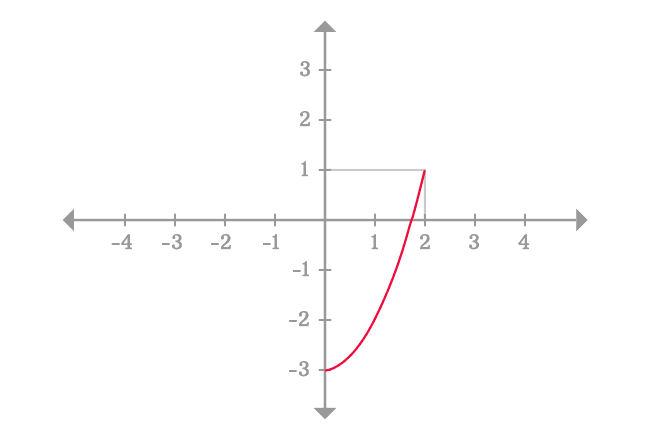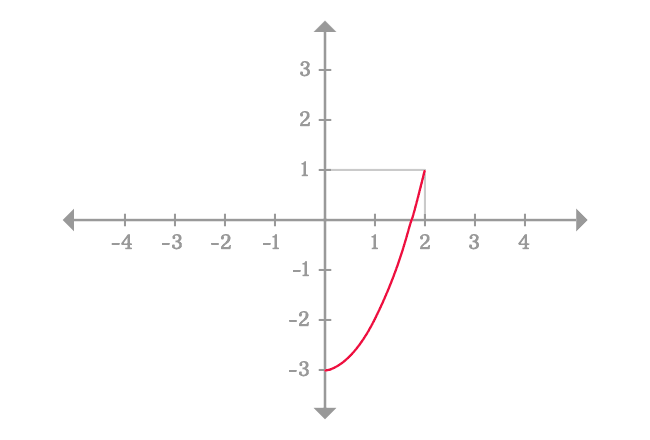
So, we have to consider the points, which are very closer to the point $x = 2$, for example $x = 1.99$ $,$ $1.999$ $,$ $1.9999$ and so on.

1. $f(1.99)$ $=$ $(1.99)^2-3$ $=$ $0.9601$
2. $f(1.999)$ $=$ $(1.999)^2-3$ $=$ $0.996001$
3. $f(1.9999)$ $=$ $(1.9999)^2-3$ $=$ $0.99960001$
4. $f(1.99999)$ $=$ $(1.9999)^2-3$ $=$ $0.9999600001$

For $x = 1.99$ $,$ $1.999$ $,$ $1.9999$ and $1.99999$, the values of the function are $0.9601$, $0.996001$, $0.99960001$ and $0.99996$ respectively.

In fact, $1.99$ $\ne$ $1.999$ $\ne$ $1.9999$ $\ne$ $1.99999$ but $1.99 \approx 2$ $,$ $1.999 \approx 2$ $,$ $1.9999 \approx 2$ and $1.99999 \approx 2$. Similarly, $0.9601$ $\ne$ $0.996001$ $\ne$ $0.99960001$ $\ne$ $0.99996$ but $0.9601 \approx 1$ $\,$ $0.996001 \approx 1$ $,$ $0.99960001 \approx 1$ and $0.9999600001 \approx 1$.

For better understanding, it is displayed in a tabular form.

$\Large x$		$f(x)$
$Actual$	$Approximate$	$Actual$	$Approximate$
$0$	$0$	$-3$	$-3$
$1$	$1$	$-2$	$-2$
$1.9$	$1.9$	$0.61$	$0.61$
$1.99$	$2$	$0.9601$	$1$
$1.999$	$2$	$0.996001$	$1$
$1.9999$	$2$	$0.99960001$	$1$
$1.99999$	$2$	$0.9999600001$	$1$
$\vdots$	$\vdots$	$\vdots$	$\vdots$

Mathematically, the values of the function are not equal but each value is approximately same and it is equal to $1$ because the value of $x$ is very closer to $2$. Therefore, you can take any value of $x$ as $x$ approaches $2$ from left hand side for calculating the limit.

For example, take $x = 1.99999$. It approaches to $2$ and left-side in the Cartesian coordinate system.

$\displaystyle \large \lim_{x \,\to\, 2^-}{\normalsize x^2-3}$ $\,=\,$ $(1.99999)^2-3$

$\implies$ $\displaystyle \large \lim_{x \,\to\, 2^-}{\normalsize x^2-3}$ $\,=\,$ $3.9999600001-3$

$\implies$ $\displaystyle \large \lim_{x \,\to\, 2^-}{\normalsize x^2-3}$ $\,=\,$ $0.9999600001$

$\,\,\, \therefore \,\,\,\,\,\,$ $\displaystyle \large \lim_{x \,\to\, 2^-}{\normalsize x^2-3}$ $\,\approx\,$ $1$

Therefore, the limit of the function $x^2-3$ as $x$ approaches $2$ from left side is equal to one and it is called the left-hand limit or left-sided limit.

Remember, $x \,\to\, 2^-$ means $x \ne 2$ and $x \ne -2$ but $x < 2$ and $x \approx 2$ in this case.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.