x-axis of two dimensional Cartesian coordinate system

A number line that displayed in horizontal position in a two-dimensional Cartesian coordinate system is called the $x$-axis of two dimensional space.

Introduction

In Bi-dimensional Cartesian coordinate system, two number lines are bisected at their middle point. One number line is drawn horizontally for measuring the distance of a point from origin in horizontal direction and the number-line is called the $x$-axis of the two dimensional Cartesian coordinate system.

Example

In this example, the $x$-axis is represented by the number line $X’OX$.

Parts

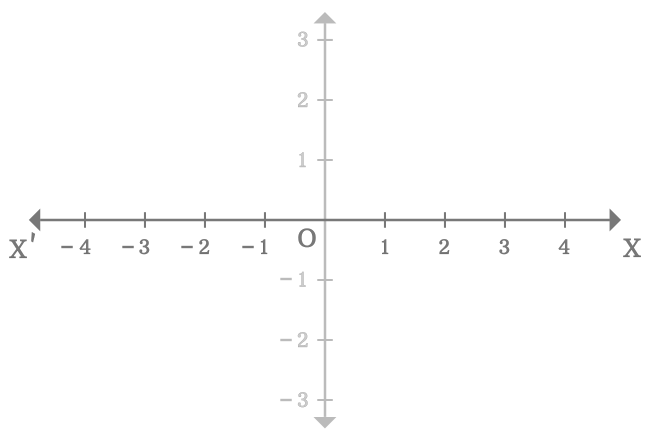
In two-dimensional space, the vertical number-line divides the $x$-axis as two parts at origin $(O)$.

Positive x-axis

The part of the $x$-axis that appears right side of the origin is called the positive $x$-axis. In this case, the ray $\overrightarrow{OX}$ is the positive $x$-axis. Each division in the positive $x$-axis is denoted by the positive integers.

Negative x-axis

The part of the $x$-axis that appears left side of the origin is called the negative $x$-axis. In this case, the ray $\overrightarrow{OX’}$ is the negative $x$-axis. Each division in the negative $x$-axis is denoted by the negative integers.

Usage

In two-dimensional Cartesian coordinate system, the $x$-axis is used to know the distance of any point from the origin by comparing the horizontal distance of the point with the number-line on the $x$-axis. For example, $A$, $B$, $C$ and $D$ are four points in a two-dimensional space.

1. The point $A$ is a point above the positive $x$-axis but it is $2$ units away from the origin.
2. The point $B$ is a point below the positive $x$-axis but it is also $2$ units away from the origin.
3. The point $C$ is a point above the negative $x$-axis but it is $3$ units away from the origin.
4. The point $D$ is a point below the negative $x$-axis but it is $4$ units away from the origin.

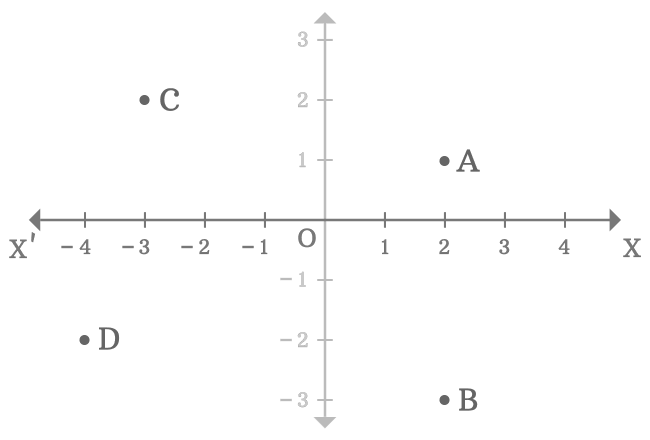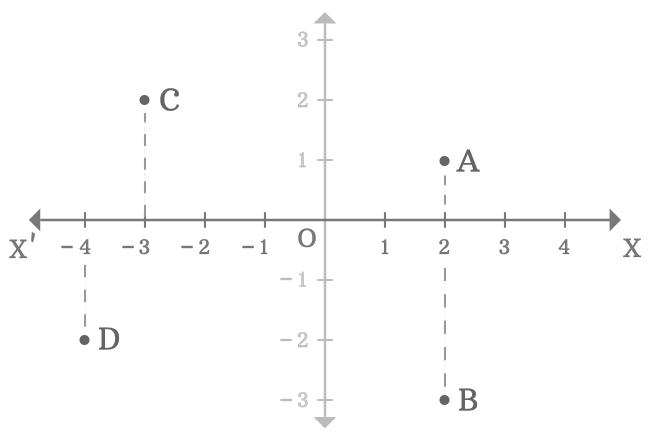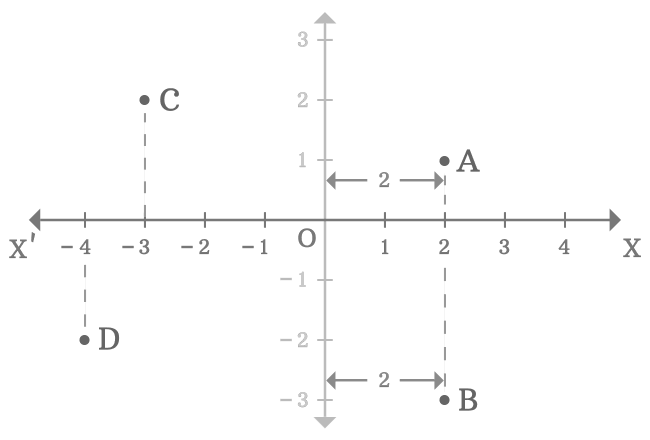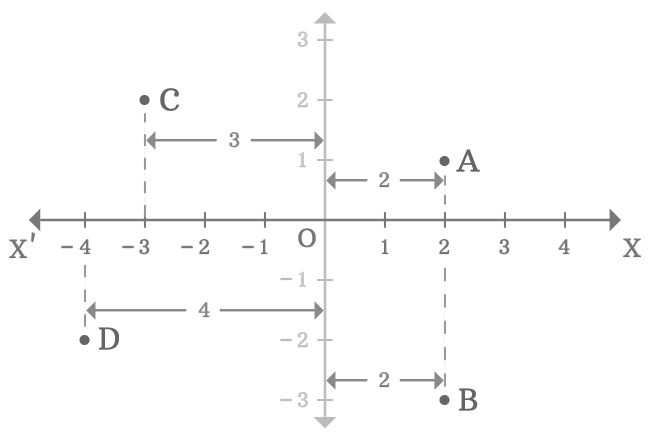
Thus, the $x$-axis is used to measure the distance of any point from the origin in horizontal direction by comparison.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.