Collinearity of 3 Points

Formula

$A(x_{1}, y_{1})$, $B(x_{2}, y_{2})$ and $C(x_{3}, y_{3})$ are three points, and the condition for the collinearity of them is

$\dfrac{y_{2}-y_{1}}{x_{2}-x_{1}} \,=\, \dfrac{y_{3}-y_{2}}{x_{3}-x_{2}}$

Proof

$A(x_{1}, y_{1})$, $B(x_{2}, y_{2})$ and $C(x_{3}, y_{3})$ are three points on a straight line in two dimensional Cartesian coordinate system. The three points are known as collinear points geometrically. Let’s try to derive a condition for the collinearity of three points mathematically.

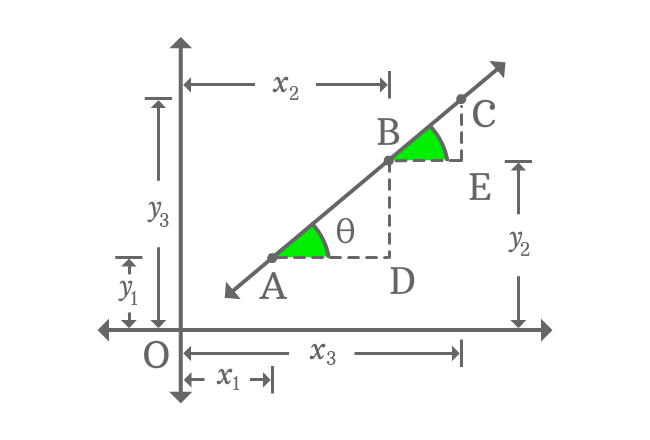
Draw parallel lines to horizontal $x$-axis from points $A$ and $B$. Similarly, draw lines from points $B$ and $C$ but they should be perpendicular to $x$-axis. The parallel and perpendicular lines get intersected at points $D$ and $E$.

It forms two right triangles, known as $\Delta DAB$ and $\Delta EBC$ in two dimensional space.

Geometrically, $\overline{AD} \,\|\, \overline{BE}$ and the two line segments $\overline{AB}$ and $\overline{BC}$ are part of the straight line. Therefore, $\angle DAB$ and $\angle EBC$ are congruent. If $\angle DAB = \theta$, then $\angle EBC = \theta$.

According to ΔDAB

Find the slope of the straight line $\overleftrightarrow{AB}$ from right triangle $DAB$.

$\tan{\theta} \,=\, \dfrac{BD}{AD}$

$\implies \tan{\theta} \,=\, \dfrac{OB-OD}{OD-OA}$

$\,\,\, \therefore \,\,\,\,\,\, \tan{\theta} \,=\, \dfrac{y_{2}-y_{1}}{x_{2}-x_{1}}$

According to ΔEBC

Find the slope of the straight line $\overleftrightarrow{BC}$ from right triangle $EBC$.

$\tan{\theta} \,=\, \dfrac{EC}{BE}$

$\implies \tan{\theta} \,=\, \dfrac{OC-OE}{OE-OB}$

$\,\,\, \therefore \,\,\,\,\,\, \tan{\theta} \,=\, \dfrac{y_{3}-y_{2}}{x_{3}-x_{2}}$

Condition of Collinearity

We know that $\overline{AB}$ and $\overline{BC}$ are part of the straight line $\overleftrightarrow{AC}$. So, the slopes of straight lines $\overleftrightarrow{AB}$ and $\overleftrightarrow{BC}$ are equal.

$\,\,\, \therefore \,\,\,\,\,\, \dfrac{y_{2}-y_{1}}{x_{2}-x_{1}} \,=\, \dfrac{y_{3}-y_{2}}{x_{3}-x_{2}}$

The mathematical equation in algebraic form represents a condition for the collinearity of three points and it is useful to us to verify the collinearity of three or more points mathematically.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.