Adjacent Angles

Two angles formed by the three lines which have a common arm and a common vertex, are defined adjacent angles.

Two angles can be formed by the lines which are started from a point. Three lines should be required to form two angles and the three lines form two angles only when one of endpoints of three lines are connected at a point and the other endpoints of them are located at different positions on a plane.

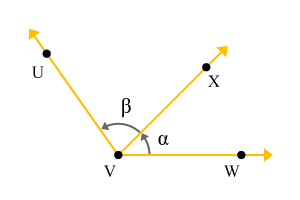
The point at which one of endpoints of three lines are joined, is called a common vertex. The middle line becomes a common arm to the first and last lines. The first and last lines make two angles with a common arm and they are adjacent to each other. Due to this reason, the angles are called adjacent angles.

Example

Consider three lines and join one of the endpoints of them at a point, which is called a vertex. Let us call it point $V$. one of points on the lines are located at $U$, $W$ and $X$ on a plane. Thus, three rays $\overrightarrow{VW}$, $\overrightarrow{VX}$ and $\overrightarrow{VU}$ are formed geometrically on a plane.

Assume, the angle between the rays $\overrightarrow{VW}$ and $\overrightarrow{VX}$ is $\alpha$. In other words $\angle XVW=\alpha$

Assume, the angle between the rays $\overrightarrow{VU}$ and $\overrightarrow{VX}$ is $\beta$. In other words $\angle UVX=\beta$

Observe the figure and the ray $\overrightarrow{VX}$ is a common arm which helps the other rays to make two angles but all three rays are started from a common vertex ($V$). Therefore, the two angles $\alpha$ and $\beta$ are called adjacent angles.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.