Supplementary angles

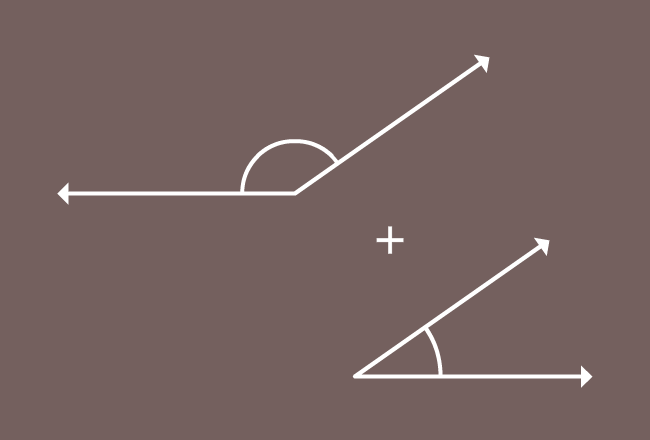
The angles whose sum equals to $180^\circ$ are called the supplementary angles.

Introduction

Supplementary angles are basically two angles but the sum of them represents a straight angle when the angles are added to each other.

One angle is known as supplement of another angle and vice-versa.

Formula

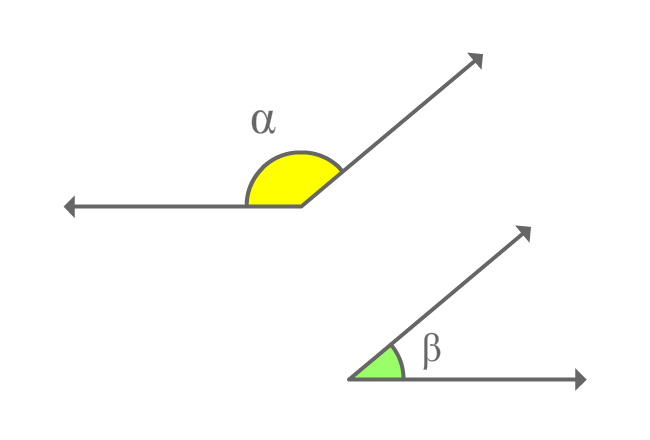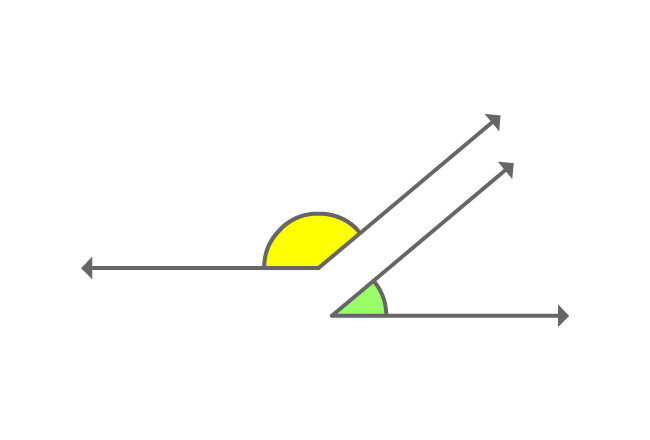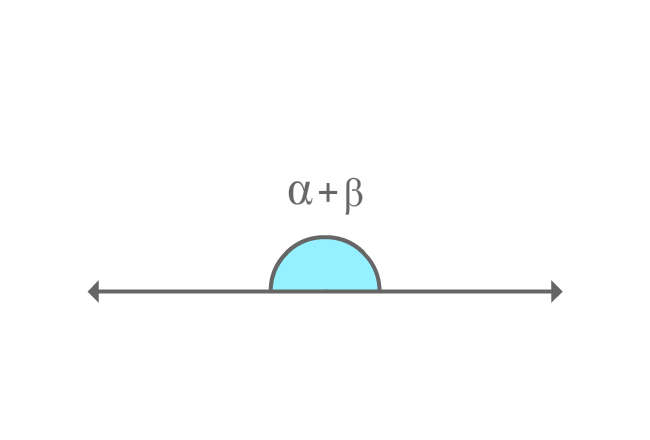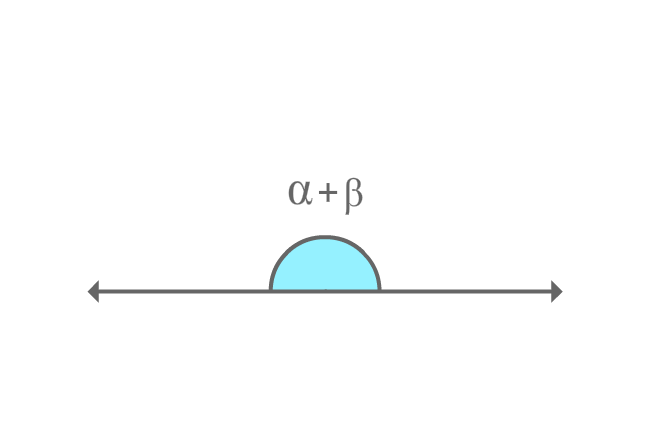
$\alpha$ and $\beta$ are two angles and the sum of them forms a straight angle geometrically.

$\alpha+\beta = 180^\circ$

1. $\alpha$ is called as supplement of $\beta$
2. $\beta$ is called as supplement of $\alpha$

The two angles $\alpha$ and $\beta$ are known as supplementary angles.

Example

$\Delta PQR$ is a triangle and the side $\overline{RS}$ splits this triangle as two triangles $\Delta PSR$ and $\Delta QSR$.

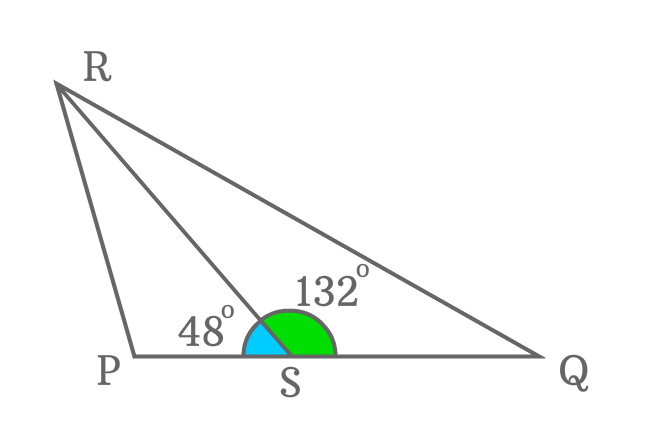
Measures $\angle PSR$ and $\angle QSR$ by using protractor.

It is measured that the $\angle PSR$ is equal to $48^\circ$ and the $\angle QSR$ is equal to $132^\circ$. Now, add both angles to get sum of them.

$\angle PSR + \angle QSR$ $=$ $48^° + 132^°$

$\implies$ $\angle PSR + \angle QSR$ $=$ $180^°$

The sum of the two angles is straight angle ${(\pi)}$. Therefore, the angles ($\angle PSR$ and $\angle QSR$) are called as supplementary angles.

The $\angle PSR$ is called as supplement of the $\angle QSR$. Similarly, $\angle QSR$ is called as supplement of the $\angle PSR$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.