Proof for Sine by Cosine Quotient identity

According to the quotient of sine by cosine identity, the quotient of sine by cosine is equal to tangent.

$\dfrac{\sin{\theta}}{\cos{\theta}} \,=\, \tan{\theta}$

This quotient trigonometric identity is derived in mathematical form geometrically from a right triangle. Now, it is your turn to learn how to prove the quotient of sine by cosine trigonometric identity from a geometric shape right angled triangle.

$\Delta BAC$ is a right triangle. In this triangle, $\overline{BC}$, $\overline{AB}$ and $\overline{AC}$ are opposite side, adjacent side and hypotenuse respectively. The angle of triangle is taken as theta.

Define Sine and Cosine functions

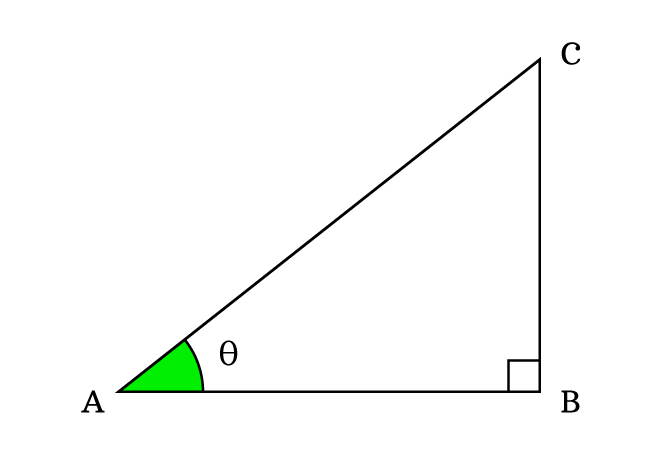
According to the definitions of the trigonometric functions, write the sine and cosine functions in ratio form at an angle theta.

$\sin{\theta} \,=\, \dfrac{BC}{AC}$

$\cos{\theta} \,=\, \dfrac{AB}{AC}$

Divide the Sine by Cosine function

Now, divide the sine function by cosine function to obtain the quotient of them.

$\dfrac{\sin{\theta}}{\cos{\theta}} \,=\, \dfrac{\dfrac{BC}{AC}}{\dfrac{AB}{AC}}$

$\implies$ $\dfrac{\sin{\theta}}{\cos{\theta}}$ $\,=\,$ $\dfrac{BC}{AC} \times \dfrac{AC}{AB}$

$\implies$ $\dfrac{\sin{\theta}}{\cos{\theta}}$ $\,=\,$ $\dfrac{BC}{AB} \times \dfrac{AC}{AC}$

$\implies$ $\dfrac{\sin{\theta}}{\cos{\theta}}$ $\,=\,$ $\dfrac{BC}{AB} \times \require{cancel} \dfrac{\cancel{AC}}{\cancel{AC}}$

$\implies$ $\dfrac{\sin{\theta}}{\cos{\theta}}$ $\,=\,$ $\dfrac{BC}{AB} \times 1$

$\implies$ $\dfrac{\sin{\theta}}{\cos{\theta}}$ $\,=\,$ $\dfrac{BC}{AB}$

Express the Ratio in Trigonometric function

In the above step, it is derived that the ratio of sine by cosine is equal to the quotient of lengths of opposite side ($BC$) by adjacent side ($AB$).

$\dfrac{\sin{\theta}}{\cos{\theta}}$ $\,=\,$ $\dfrac{BC}{AB}$

As per trigonometry, the quotient of $BC$ by $AB$ represents the tangent. In this case, the angle of right triangle is theta. Hence, the tan function is written as $\tan{\theta}$.

$\,\,\,\therefore\,\,\,\,\,\,$ $\dfrac{\sin{\theta}}{\cos{\theta}}$ $\,=\,$ $\tan{\theta}$

Therefore, it is proved that the quotient of sine function by cosine function is equal to the tangent function mathematically.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.