$\sin{(45^\circ)}$ value’s Proof

There are two ways to find the value of sin of $45$ degrees in trigonometry. The two methods are based on geometry but approach is slightly different.

Theoretical approach

There is a geometric property which describes the relation between opposite and adjacent sides when angle of right triangle is $45^\circ$. The lengths of opposite and adjacent sides are equal when angle of right triangle equals to $45^\circ$. This property helps us to find the value of $\sin{(45^\circ)}$ exactly in trigonometry.

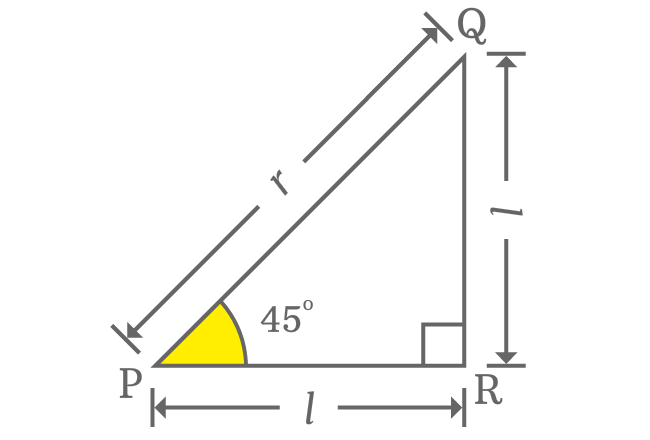
Assume, the length of both opposite side and adjacent side is represented by $l$ and the length of hypotenuse is denoted by $r$. Now, express Pythagorean Theorem in terms of them.

$r^2 = l^2 + l^2$

$\implies r^2 = 2l^2$

$\implies r = \sqrt{2}.l$

$\implies \dfrac{l}{r} = \dfrac{1}{\sqrt{2}}$

$l$ and $r$ are lengths of opposite side (or adjacent side) and hypotenuse respectively.

$\implies \dfrac{Length \, of \, Opposite \, side}{Length \, of \, Hypotenuse} = \dfrac{1}{\sqrt{2}}$

The ratio is actually calculated when angle of right triangle is $45^\circ$. Therefore, the ratio of lengths of opposite side to hypotenuse is $\sin{\Big(\dfrac{\pi}{4}\Big)}$.

$\therefore \,\,\, \sin{(45^\circ)} = \dfrac{1}{\sqrt{2}}$

$\sin{(45^\circ)} = \dfrac{1}{\sqrt{2}} = 0.7071067812\ldots$

Practical approach

You can also find the value of sine of angle $45^\circ$ practically by drawing a right triangle with geometric tools.

1. Draw a horizontal line from Point $F$.
2. Take Protractor, coincide point $F$ with centre and also coincide the horizontal line with right side base line of protractor. Then mark a point at $45$ degrees.
3. Take ruler and draw a line from point $F$ through $45^\circ$ angle’s marked point.
4. Take compass and set its length to any length (for example $7 cm$) by ruler. Then draw an arc on $45^\circ$ angle line from point $F$. It cuts the $45$ degrees line at point $G$.
5. Finally, draw a perpendicular line to horizontal line from point $G$ and it intersects the horizontal line at point $H$. It formed a right triangle, known as $\Delta GFH$

Now, calculate the value of $\sin{(50^g)}$ by measuring the lengths of opposite side and hypotenuse of right triangle $GFH$ by a ruler.

$\sin{(45^\circ)} = \dfrac{Length \, of \, Opposite \, side}{Length \, of \, Hypotenuse}$

$\implies \sin{(45^\circ)} \,=\, \dfrac{GH}{FG}$

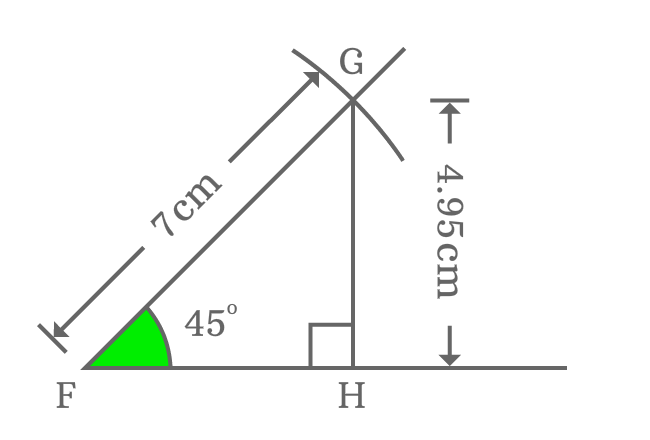
In this example, the length of hypotenuse ($FG$) is $7cm$ and the length of opposite side is measured as $4.95$ centimetres by ruler. Finally, calculate the ratio between them to get the value of sine of angle $45$ degrees geometrically.

$\implies \sin{(45^\circ)} \,=\, \dfrac{GH}{FG} = \dfrac{4.95}{7}$

$\,\,\, \therefore \,\,\,\,\,\, \sin{(45^\circ)} \,=\, 0.7071428571\ldots$

Verdict

The value of $\sin{(45^\circ)}$ is derived as $0.7071067812\ldots$ in theoretical approach but the value of $\sin{(45^\circ)}$ is derived as $0.7071428571\ldots$ in practical approach. There is a slight difference between them when they are compared.

Actually, there is some error in measuring the length of the opposite side and it creates problem to find the exact value of $\sin{(45^\circ)}$ in practical geometric approach but it can be obtained exactly in theoretical approach because of considering the direct relation between lengths of opposite side and hypotenuse.

However, the approximate value of $\sin{\Big(\dfrac{\pi}{4}\Big)}$ in both theoretical and practical approaches is same and is equal to $0.7071$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.