Properties of Right triangle when angle equals to 45°

Properties

There are three properties of a right triangle when angle of right angled triangle is equal to $45$ degrees.

1. The lengths of opposite and adjacent sides are equal.
2. Lengths of hypotenuse is $\small \sqrt{2}$ times to both opposite and adjacent sides.
3. Complementary angles are equal.

Theorem

$\Delta ECD$ is a right triangle, which contain an angle of $45^°$. Let us take, the length of opposite side is $d$.

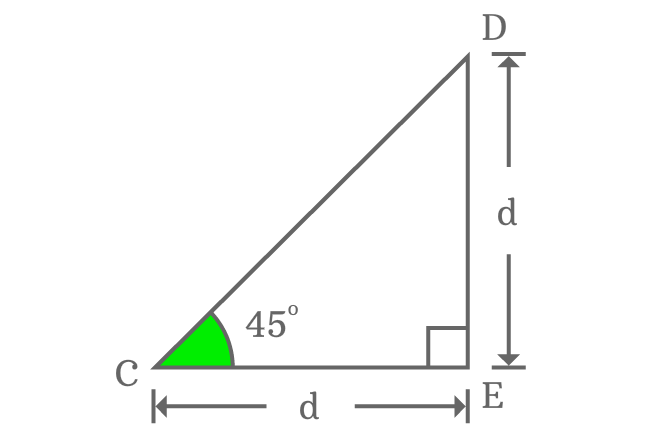
Geometrically, the lengths of both opposite side and adjacent side are equal when angle of right triangle is $45$ degrees.

$Length \, of \, Opposite \, side$ $\,=\,$ $Length \, of \, Adjacent \, side$ $\,=\,$ $d$

The lengths of opposite and adjacent sides are known. So, the length of hypotenuse can be calculated by using Pythagorean Theorem.

${CD}^2 \,=\, {CE}^2 + {DE}^2$

$\implies$ ${CD}^2 \,=\, d^2 + d^2$

$\implies$ ${CD}^2 \,=\, 2d^2$

$\implies$ $CD \,=\, \sqrt{2d^2}$

$\,\,\, \therefore \,\,\,\,\,\,$ $CD \,=\, \sqrt{2}d$

Theoretically, it is proved that the length of hypotenuse is equal to square root of two times of either length of opposite side (perpendicular) or adjacent side (base).

The interior angles of triangle is $180^°$. On the basis of this rule, an angle of triangle can be calculated when its two angles are known. An angle is a right angle and the angle of right triangle is $45$ degrees . So, the remaining third angle can be calculated by applying sum of angles of triangle rules.

$\angle CDE + \angle DEC + \angle ECD$ $\,=\,$ $180^°$

$\implies \angle CDE + 90^° + 45^°$ $\,=\,$ $180^°$

$\implies \angle CDE + 135^°$ $\,=\,$ $180^°$

$\implies \angle CDE$ $\,=\,$ $180^°-135^°$

$\,\,\, \therefore \,\,\,\,\,\, \angle CDE$ $\,=\,$ $45^°$

Proof

The three properties of right triangle can also be derived to prove geometrically by constructing a right triangle with an angle of $45$ degrees.

1. Draw a line horizontally from point $\small I$ in a plane.
2. Take protractor and draw a $45$ degrees line from $\small I$ by a ruler.
3. Use compass and set its length to any length (for example $6 \, cm$) by a ruler. After that, draw an arc on $45^°$ line from point $\small I$ and it intersects the $45^°$ line at point $\small J$.
4. Later, draw a perpendicular line to horizontal line from point $\small J$ and it intersects the horizontal line at point $\small K$. In this way, a right triangle ($\small \Delta KIJ$) is constructed geometrically.

The geometrical properties of right angled triangle when its angle equals to $45^{°}$ can be proved geometrically.

Property

The lengths of opposite and adjacent sides are equal when angle of a right triangle is $\dfrac{\pi}{4}$

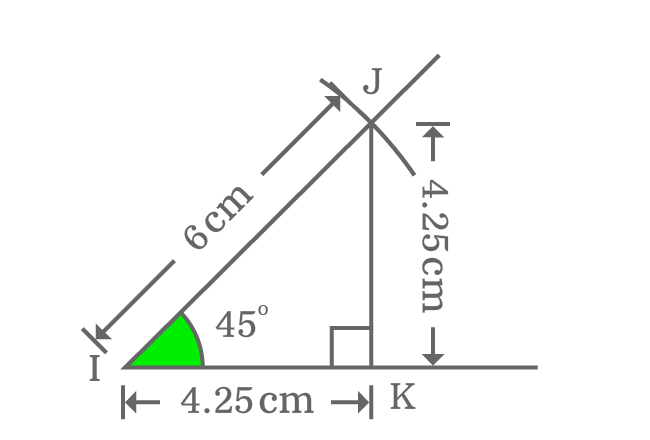
Measure the lengths of both opposite side and adjacent side by a ruler. You will observe that the lengths of both sides are equal and length of each of them is $4.25 \, cm$ exactly.

Now, calculate the length of either opposite side or adjacent in theoretical method.

$Length \, of \, Opposite \, side$ $\,=\,$ $\dfrac{Length \, of \, Hypotenuse}{\sqrt{2}}$

$Length \, of \, Opposite \, side$ $\,=\,$ $\dfrac{6}{\sqrt{2}}$

$\implies Length \, of \, opposite \, side$ $\,=\,$ $4.2426\ldots$

$\,\,\, \therefore \,\,\,\,\,\, Length \, of \, opposite \, side$ $\, \approx \,$ $4.24$

The length of either opposite or adjacent side is $4.25 \, cm$ geometrically and the approximate value of it in theoretical method is $4.24 \, cm$. The two values are equal approximately.

Therefore, it is proved that the lengths of opposite and adjacent sides are equal when angle of right triangle is $45$ degrees.

Property

The length of hypotenuse equals to square root of two times of length of either opposite or adjacent side when angle of right triangle is $45$ degrees.

The length of both opposite and adjacent sides is $4.25 \, cm$. Now, Pythagorean Theorem and calculate the length of hypotenuse mathematically.

$Length \, of \, Hypotenuse$ $\,=\,$ $\sqrt{{(4.25)}^2 + {(4.25)}^2}$

$\implies Length \, of \, Hypotenuse$ $\,=\,$ $\sqrt{2 \times {(4.25)}^2 }$

$\implies Length \, of \, Hypotenuse$ $\,=\,$ $\sqrt{2} \times 4.25$

$\,\,\, \therefore \,\,\,\,\,\, Length \, of \, Hypotenuse$ $\,=\,$ $\sqrt{2} \times $ $Length \, of \, Opposite \, (or) \, Adjacent \, side$

Property

Complementary angles of right triangle are equal when angle of right triangle is $45$ degrees.

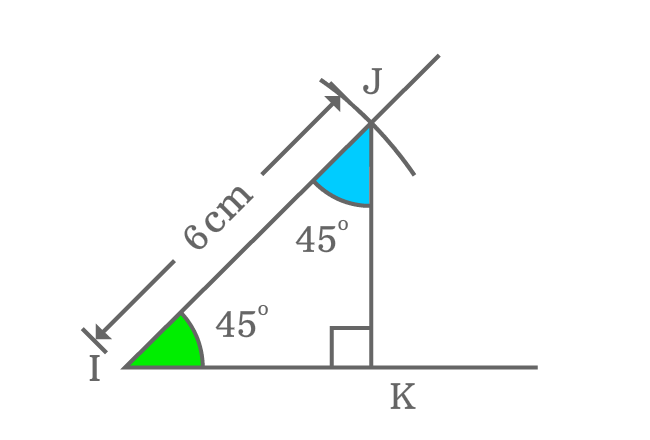
$\angle KIJ$ and $\angle IJK$ are two angles and complementary angles of right triangle. The $\angle KIJ$ is $45$ degrees and it is angle of right triangle. $\angle IJK$ is complementary angle of $\angle KIJ$ but unknown.

It can be known by measuring $\angle IJK$ by a protractor. You’ll observe that the angle of $IJK$ is also $45$ degrees.

Therefore, it is proved that the complementary angles are equal in a right angle when its angle is equal to $45$ degrees and the sum of the complementary angles is a right angle.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.