Proof of $\sin{(36^\circ)}$ value in Geometric method

The sine of angle thirty six degrees is proved in trigonometric method exactly as the square root of ten minus two times square root of five by four.

$\sin{(36^\circ)}$ $\,=\,$ $\dfrac{\sqrt{10-2\sqrt{5}}}{4}$

Geometrically, the sine of angle thirty six degrees value can also be derived by constructing a right triangle with an angle thirty six degrees but it is impossible to evaluate the exact value of sin pi by five value due to the problem in measuring the lengths of the sides. However, its value can be derived approximately.

1. Draw a line horizontally by a ruler. You can draw it with any length. In this example, a horizontal line is drawn with $6\,cm$ length from the point $H$ to $I$.
2. Set the center (or centre) of protractor to coincide with point $H$ and also coincide its right side base line with horizontal line. Later, draw a straight line with thirty six degrees from point $H$.
3. Now, draw a perpendicular line to horizontal line in top side direction from point $I$ and it intersects the thirty six degrees line at point $J$.

According to the above three steps, a right angled triangle (or right triangle) can be constructed geometrically with an angle of pi by five radian. Now, we can start the mathematical procedure to evaluate the sine of angle thirty six degrees value.

On the basis of $\Delta JHI$, the sine of angle thirty six degrees can be expressed in ratio form of the sides as per its fundamental definition. In this triangle, the opposite side and hypotenuse are $\overline{JI}$ and $\overline{HJ}$ respectively.

$\sin{(36^\circ)}$ $\,=\,$ $\dfrac{JI}{HJ}$

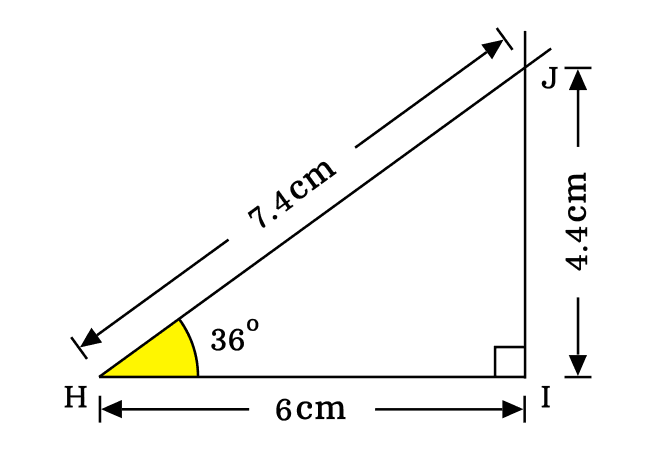
Actually, the lengths of opposite side and hypotenuse are unknown. So, it is not possible to evaluate the sine of forty grades value mathematically. Hence, measure the lengths of them by a ruler. It is measured that the length of opposite side is $4.4\,cm$ and hypotenuse is $7.4\,cm$.

$\implies$ $\sin{(36^\circ)}$ $\,=\,$ $\dfrac{4.4}{7.4}$

$\implies$ $\sin{(36^\circ)}$ $\,=\,$ $0.5945945945\cdots$

$\,\,\,\therefore\,\,\,\,\,\,$ $\sin{(36^\circ)}$ $\,\approx\,$ $0.5946$

In fact, it is not possible to derive the value of sine of angle thirty six degrees exactly in geometric approach but can only be obtained approximately.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.