$\sin{(0^°)}$ Proof

According to trigonometry, the exact value of sine of zero degrees is equal to zero.

$\sin{(0^°)} \,=\, 0$

The sine of angle zero degrees can be derived in mathematics in two different geometric approaches. Now, it is your time to learn how to derive the sine of angle zero radian value mathematically.

Fundamental method

The sine of angle zero degrees can be derived theoretically by considering a geometric property of a side in a zero degrees right triangle. Now, imagine a right triangle that contains zero degrees angle. The $\Delta RPQ$ is an example for a right triangle with zero angle.

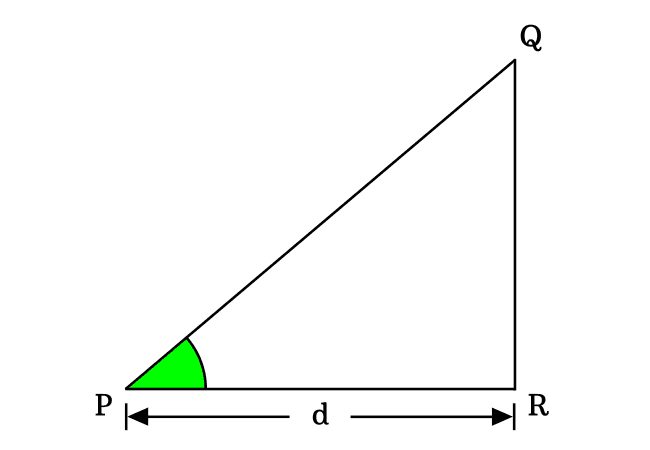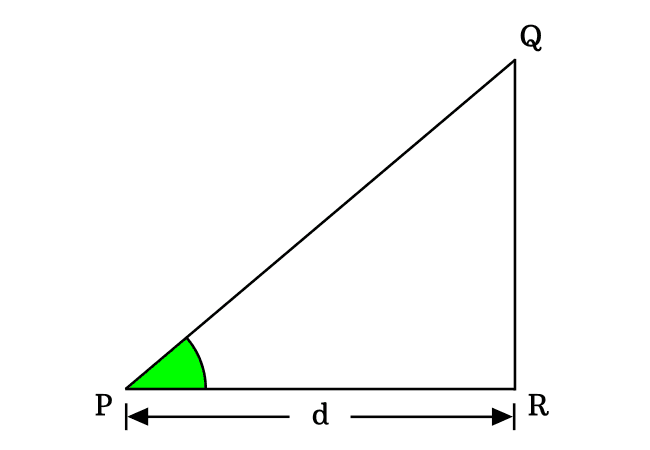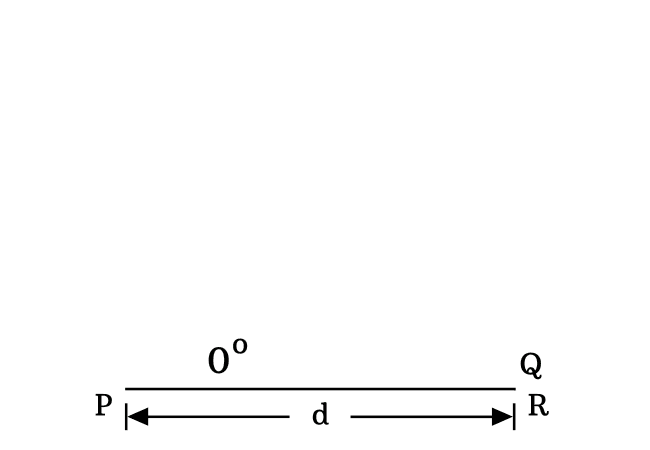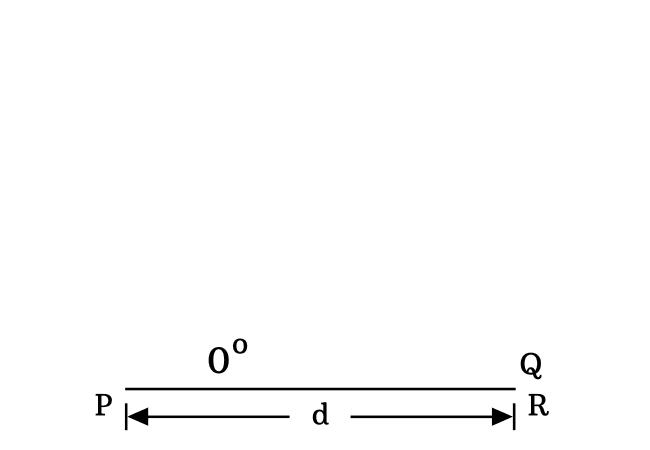
According to the fundamental definition of the sin function, it can be expressed in ratio form of lengths of the opposite side and hypotenuse. In fact, the sine function is written as $\sin{(0^°)}$ when the angle of a right triangle is zero grades.

$\implies$ $\sin{(0^°)}$ $\,=\,$ $\dfrac{Length \, of \, Opposite \, side}{Length \, of \, Hypotenuse}$

$\implies$ $\sin{(0^°)}$ $\,=\,$ $\dfrac{QR}{PQ}$

In a zero degree right triangle, the length of opposite side is zero. It means $QR \,=\, 0$.

$\implies$ $\sin{(0^°)}$ $\,=\,$ $\dfrac{0}{d}$

$\,\,\,\therefore\,\,\,\,\,\,$ $\sin{(0^°)}$ $\,=\,$ $0$

Experimental method

The sin of angle zero degrees is also proved practically with geometric tools by constructing a right triangle with zero degrees angle. Now, let’s start the process for constructing a right angled triangle with zero degrees angle.

1. Draw a straight line horizontally from point $A$ in the plane.
2. Take protractor and draw a zero degrees line by coinciding the point $A$ with its middle point and also coinciding the right side base line with horizontal line. In this case, the zero degree angle line is drawn over the horizontal line.
3. Set the compass to any length by a ruler. In this example, The distance between lead point and pencil point to $5 \, cm$. Now, draw an arc on zero angle line from point $A$ and it intersects the point at point $B$.
4. Use set square and draw a perpendicular line to horizontal line from point $B$ and it intersects the horizontal line at point $C$. Thus, $\Delta BAC$ is constructed geometrically by the geometric tools.

The opposite side, adjacent side and hypotenuse are $\overline{BC}$, $\overline{AC}$ and $\overline{AB}$ respectively in $\Delta BAC$.

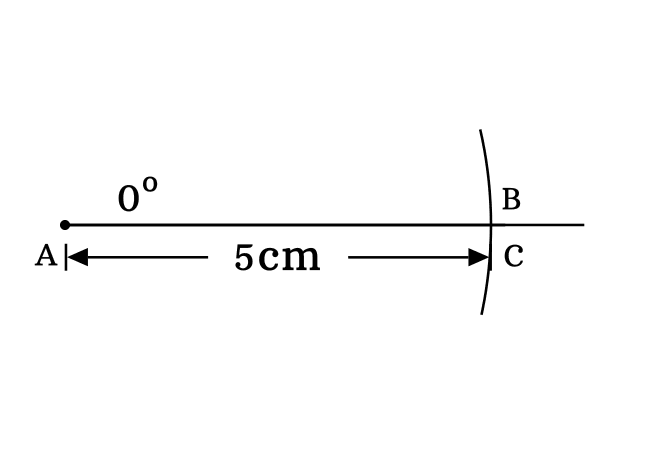
It is time to find the value of $\sin{(0)}$ by calculating the ratio of lengths of opposite side to hypotenuse of the right triangle $BAC$.

$\sin{(0^°)} = \dfrac{Length \, of \, Opposite \, side}{Length \, of \, Hypotenuse}$

$\implies \sin{(0^°)} \,=\, \dfrac{BC}{AB}$

In this example, $BC \,=\, 0\,cm$, $AC \,=\, 5\,cm$ and $BC \,=\, 5\,cm$.

$\implies \sin{(0^°)} \,=\, \dfrac{BC}{AB}$

$\implies \sin{(0^°)} \,=\, \dfrac{0}{5}$

$\,\,\,\therefore \,\,\,\,\,\, \sin{(0^°)} \,=\, 0$

In this way, the sine of angle zero degrees equals to zero is proved in two different geometric methods.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.