Sides of an angle
Definition
A straight line that meets another line at a point to form an angle is called the side of an angle.
Introduction
A straight line starts from a point geometrically on a plane. Similarly, another straight line can also start from same point. The starting point of both lines is same and it is also their meeting point. The meeting of the lines at that point forms an angle between them. Now, each straight line is called the side of an angle and it is also called the arm of an angle.

Geometrically, each angle has two sides or arms possibly and it can be clearly understood from the above graphical animation. Now, you have clearly understood what the sides of an angle really are.
Example
Let’s learn the concept of the sides of an angle geometrically.
- Let’s consider a point on a plane and denote it by $O$.
- Draw a line from point $O$ and let’s assume that it passes through a point $P$.
- Similarly, draw another line from the same point and assume that it passes through a point $Q$.
The straight-line $\overrightarrow{OP}$ meets the straight line $\overrightarrow{OQ}$ at their starting point $O$, and their meeting forms an angle between them.
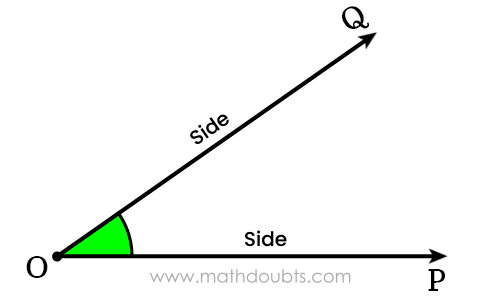
Therefore, the straight-lines $\overrightarrow{OP}$ and $\overrightarrow{OQ}$ are called the sides of angle geometrically.
Representation
The mathematical notation of an angle with examples to learn how to represent an angle in mathematics.
