$\sec{(45^°)}$ Proof

The exact value of secant of $45$ degrees is derived in geometry and it can also be derived in trigonometry by a trigonometric identity. In geometry, the $\sec{(45^°)}$ value can be derived in theoretical and practical approaches. Now, let’s learn the ways of deriving the $\sec{\Big(\dfrac{\pi}{4}\Big)}$ value in mathematics one after one.

Theoretical approach

The secant of $45$ degrees value is derived theoretically in geometry by the direct relation between lengths of opposite and adjacent sides when angle of right triangle is $45^°$. In fact, the lengths of opposite and adjacent sides are equal if the angle of right angled triangle is $50^g$.

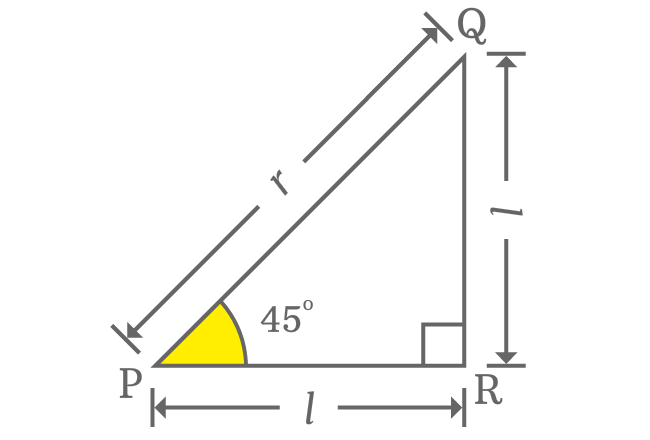
For example, $\Delta RPQ$ is a right triangle with $45^°$ angle. The length of both opposite and adjacent side is represented by $l$ and the length of hypotenuse is denoted by $r$. Now, express the lengths of all three sides mathematically by Pythagorean Theorem.

${PQ}^2 = {PR}^2 + {QR}^2$

$\implies r^2 = l^2 + l^2$

$\implies r^2 = 2l^2$

$\implies r = \sqrt{2}.l$

$\implies \dfrac{r}{l} = \sqrt{2}$

Actually, $r$ and $l$ are lengths of hypotenuse and adjacent side (or opposite side) respectively.

$\implies \dfrac{Length \, of \, Hypotenuse}{Length \, of \, Adjacent \, side} = \sqrt{2}$

This ratio of lengths of hypotenuse to adjacent side is calculated when angle of right triangle is $45^°$. Hence, it is represented by $\sec{(45^°)}$

$\therefore \,\,\, \sec{(45^°)} = \sqrt{2}$

$\sec{(45^°)} = \sqrt{2} = 1.4142135623\ldots$

Practical approach

Even though you don’t know the relation between opposite and adjacent side when angle of right triangle is $50^g$, you can evaluate the value of $\sec{\Big(\dfrac{\pi}{4}\Big)}$ approximately on your own by using geometrical tools. It is actually done by constructing a right triangle with $45$ degrees angle.

1. Draw a straight line from point $L$ horizontally.
2. Coincide the centre of protractor with point $L$ and also coincide the right side base line of protractor with horizontal line. Now, identify $45^°$ small line on protractor and put a mark on plane.
3. Draw a straight line by ruler from point $L$ through the point which indicates the $45$ degrees.
4. Take compass and set it to any length by the ruler. In this example, the compass is set to $9 \, cm$ and then draw an arc on $45$ degrees straight line from point $L$. It cuts the $45^°$ line at point $M$.
5. Later, take set square and draw a perpendicular line to horizontal line from point $M$ and it intersects the horizontal line at point $N$ perpendicularly.

The above five steps construct a right triangle, denoted by $\Delta NLM$ geometrically. Now, use the $\Delta NLM$ to find the value of $\sec{\Big(\dfrac{\pi}{4}\Big)}$ on your own by using geometrical tools.

$\sec{(45^°)} = \dfrac{Length \, of \, Hypotenuse}{Length \, of \, Adjacent \, side}$

$\implies \sec{(45^°)} \,=\, \dfrac{LM}{LN}$

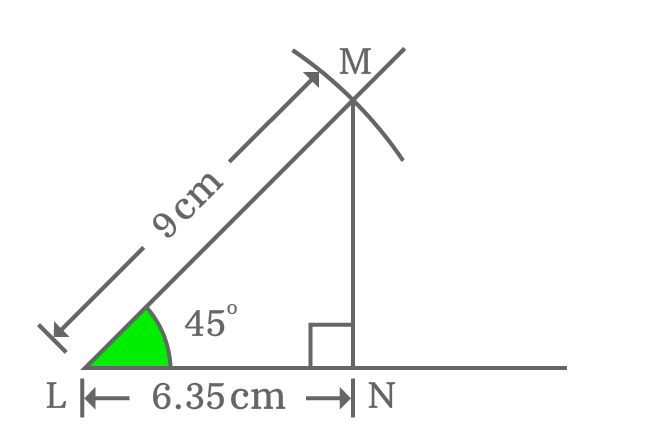
As you know that, the $\Delta NLM$ is constructed geometrically by taking the length of hypotenuse as $9 \, cm$ but the length of adjacent side is unknown. It is essential to know this for finding the value of $\sec{(50^g)}$.

The length of adjacent side can be measured by ruler and you will observe that it is nearly $6.35 \, cm$.

$\implies \sec{(45^°)} \,=\, \dfrac{LM}{LN} = \dfrac{9}{6.35}$

$\,\,\, \therefore \,\,\,\,\,\, \sec{(45^°)} \,=\, 1.4173228346\ldots$

Trigonometric approach

The value of secant of $\dfrac{\pi}{4}$ can also be derived in trigonometry by the reciprocal identity of cosine function.

$\sec{(45^°)} = \dfrac{1}{\cos{(45^°)}}$

Replace the exact value of cos of $45$ degrees in fraction form.

$\implies \sec{(45^°)} = \dfrac{1}{\dfrac{1}{\sqrt{2}}}$

$\implies \sec{(45^°)} = 1 \times \dfrac{\sqrt{2}}{1}$

$\implies \sec{(45^°)} = 1 \times \sqrt{2}$

$\,\,\, \therefore \,\,\,\,\,\, \sec{(45^°)} = \sqrt{2}$

Verdict

As per theoretical geometrical method, the value of $\sec{(45^°)}$ is $\sqrt{2}$ or $1.4142135623\ldots$ and the value $\sec{(45^°)}$ is $1.4173228346\ldots$ as per practical geometrical method. You observe that there is a slight difference between them when you compare them.

The value of $\sec{(45^°)}$, obtained from theoretical geometrical method is exact value but the value of $\sec{(45^°)}$, obtained from practical geometrical method is approximate value because it is calculated by measuring the approximate value of adjacent side by the ruler.

The approximate value of $\sec{\Big(\dfrac{\pi}{4}\Big)}$ is often considered as $1.4142$ in mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.