Minors of a $2 \times 2$ matrix

The determinant of the square sub-matrix of the order one by leaving the row and the column of an entry is called the minor of that element in the square matrix of the order two.

Introduction

In a $2 \times 2$ square matrix, there are four elements (or entries), which are arranged in two rows and two columns. If an entry is considered by ignoring the elements in its row and column, then there will still be an element in the matrix and it forms a square sub-matrix of the order one. The determinant of that first order square sub-matrix is the minor of the respective entry. So, four minors are possible in the case of the square matrix of the order $2$.

$A$ $\,=\,$ $\begin{bmatrix} e_{11} & e_{12} \\ e_{21} & e_{22} \\ \end{bmatrix}$

Now, let’s learn how to evaluate the minor for each element in the square matrix of the order $2$ fundamentally.

Minor for entry in the first row and the first column

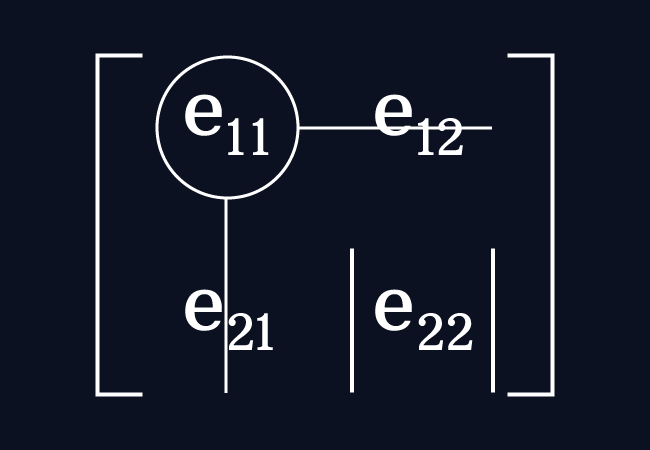
Consider the entry $e_{11}$ in the matrix $A$. It is an element in the first row and the first column.

Leave the entries in the first row and the first column. It forms a $1 \times 1$ square sub-matrix with the remaining element $e_{22}$

The determinant of the square sub-matrix of the order one is the minor of the entry $e_{11}$ and it is represented by the $M_{11}$

$M_{11} \,=\, \begin{vmatrix} e_{22} \\ \end{vmatrix}$

$\therefore \,\,\,$ $M_{11} \,=\, e_{22}$

Therefore, the minor of the element $e_{11}$ in the matrix $A$ is $e_{22}$.

Minor for entry in the first row and the second column

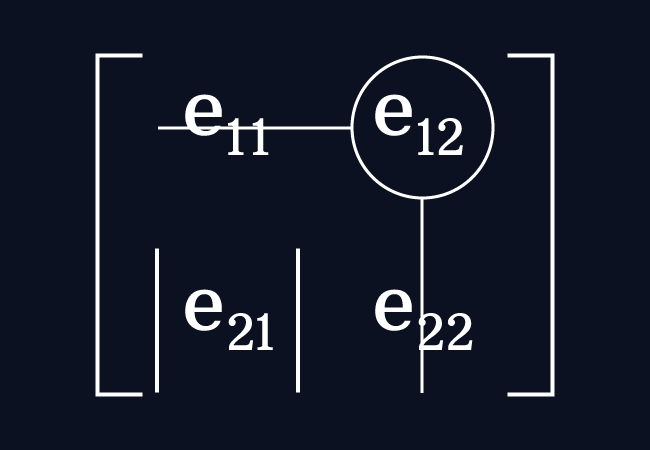
Concentrate on the element $e_{12}$ in the matrix $A$. It is an entry in the first row and the second column.

Now, ignore the elements in the first row and the second column. It forms a square sub-matrix of the order $1 \times 1$ with the remaining entry $e_{21}$.

The determinant of the square sub-matrix of the order $1$ is the minor for the element $e_{12}$ and it is denoted by the $M_{12}$.

$M_{12} \,=\, \begin{vmatrix} e_{21} \\ \end{vmatrix}$

$\therefore \,\,\,$ $M_{12} \,=\, e_{21}$

Therefore, the minor of the element $e_{12}$ in the matrix $A$ is $e_{21}$.

Minor for entry in the second row and the first column

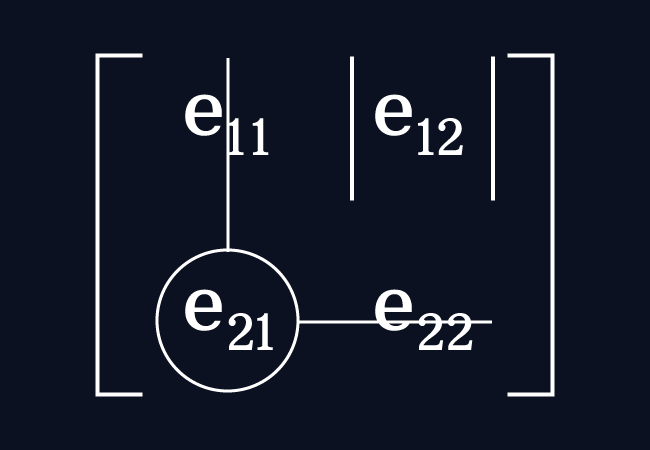
Consider the entry $e_{21}$ in the matrix $A$ and it is an element in the second row and the first column.

Now, forget the entries in the second row and the first column. It forms a $1 \times 1$ square sub-matrix with the remaining element $e_{21}$.

The determinant of the first order square sub-matrix is the minor of the element $e_{21}$ and it is represented by the $M_{21}$.

$M_{21} \,=\, \begin{vmatrix} e_{12} \\ \end{vmatrix}$

$\therefore \,\,\,$ $M_{21} \,=\, e_{12}$

Therefore, the minor of the element $e_{21}$ in the matrix $A$ is $e_{12}$.

Minor for entry in the second row and the second column

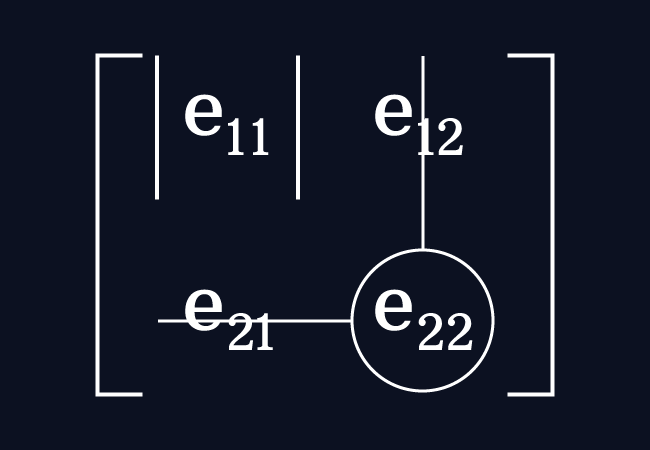
Finally, focus on the entry $e_{22}$ in the matrix $A$ and this element is an entry in the second row and the second column.

Neglect the entries in the second row and the second column. It forms a square sub-matrix, which is a matrix of the order $1 \times 1$ with the remaining element $e_{22}$.

The determinant of the square sub-matrix of the order one is the minor of the entry $e_{22}$ and it is denoted by the $M_{22}$.

$M_{22} \,=\, \begin{vmatrix} e_{11} \\ \end{vmatrix}$

$\therefore \,\,\,$ $M_{22} \,=\, e_{11}$

Therefore, the minor of the element $e_{22}$ in the matrix $A$ is $e_{11}$.

Thus, the minor for each entry in the second order square matrix is evaluated in the mathematics. It can also understand from an understandable example.