Mantissa

The fractional part of common logarithm is called mantissa.

Introduction

The logarithm of a quantity is expressed as two quantities and they are in fractional and integral forms.

Initially, the fractional part is in the form logarithm of a decimal number but later it’s transformed into another decimal number according to the logarithmic table and it’s called mantissa.

$\log{(Q)} \,=\, C + \log{(m)}$

The literal $C$ expresses characteristic and the quantity in decimal form obtained from $\log{m}$ is known as mantissa.

Note

The quantity ($m$) inside the logarithm is adjusted to a decimal number whose whole number part should be greater than or equal to $1$ but less than $10$. In other words, $1 \leq m < 10$

Therefore, $0 \leq \log{m} < 1$

Example

$6583$ is a quantity and let us find the mantissa for this quantity.

Express the quantity inside the logarithm as a decimal number but the whole number part of this decimal number should be greater than or equal to $1$ and less than $10$.

$\log{(6583)}$ $\,=\,$ $\log{(6.583 \times {10}^3)}$

The logarithm of product of two quantities can be written as sum of their logs as per product rule of logarithms.

$\implies$ $\log{(6583)}$ $\,=\,$ $\log{(6.583)}$ $+$ $\log{({10}^3)}$

Forget about logarithm of quantity in exponential form but concentrate on logarithm of decimal number to find the mantissa. Remember, we consider only first four digits of any number to find the mantissa by using log table.

1. Identify first two digits of the quantity in the first column of the logarithmic table. $65$ is first two digits in this case.
2. Consider third digit in the quantity and it is $8$. So, look at the corresponding value in the column denoted by $8$ in the row corresponding to $65$. In this case, $8182$.
3. Now, consider fourth digit in the quantity, it is $3$. In the row corresponding to $65$, look at the number in the column headed by $3$ in the mean differences section. In this case, $2$.

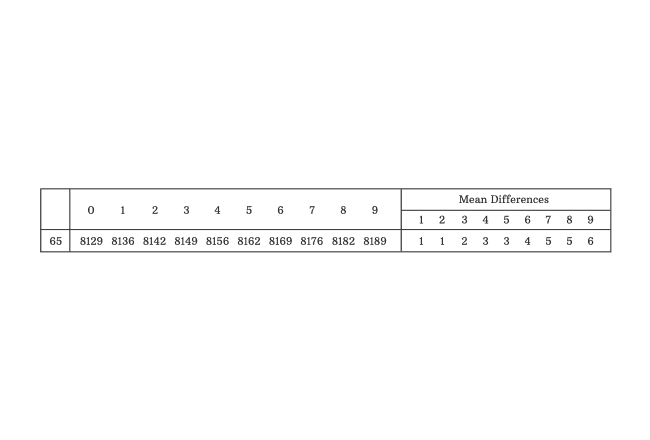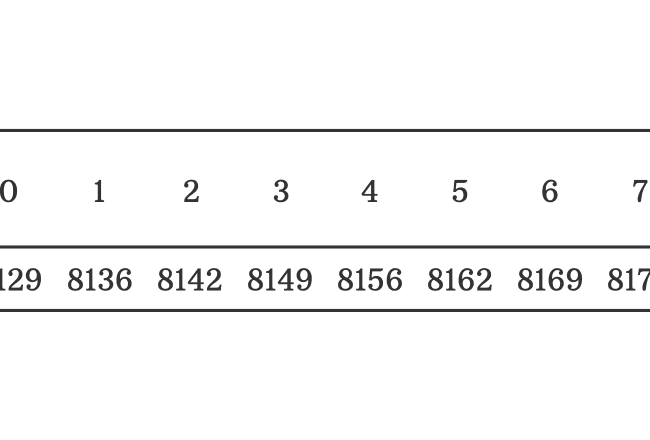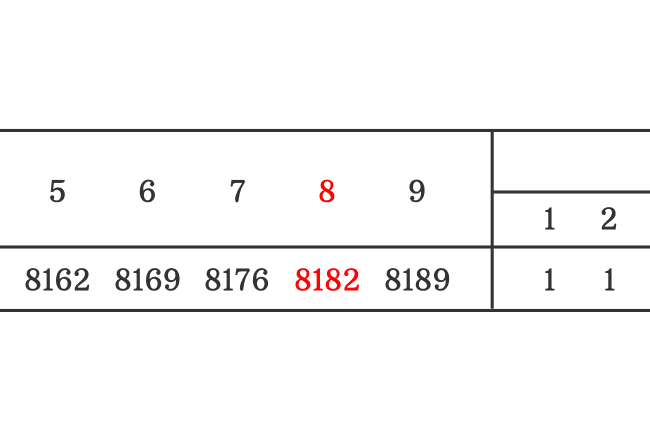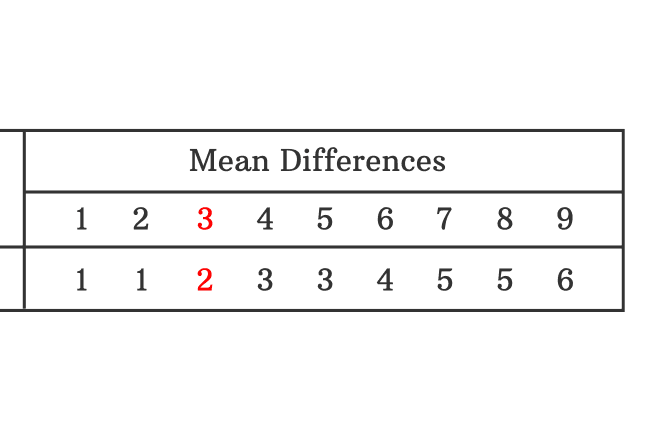
Finally, add both quantities. $8182+2 = 8184$.

The quantity inside the logarithm is $6583$ and it’s adjusted to $6.583$. It’s actually greater than or equal to $1$ and less than $10$. Hence, the logarithm of $6.583$ should be greater than or equal to $0$ but less than $1$.

Therefore, $\log{(6.583)} = 0.8184$

Therefore, the mantissa for the logarithm of number $6583$ is $0.8184$. Thus, you can find mantissa for any quantity by using logarithmic table.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.