Common Logarithm

A logarithmic system which contains $10$ as its base, is called common logarithm.

Introduction

Henry Briggs, a British mathematician who studied John Napier’s natural logarithmic system comprehensively. On the basis of natural logarithmic system, he introduced a logarithmic system by using $10$ as base of the logarithm.

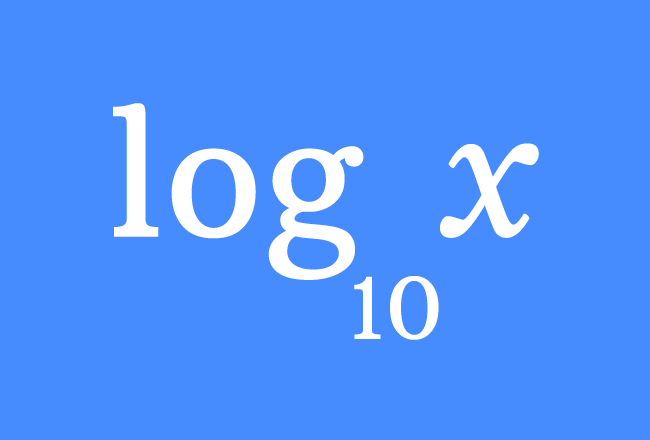
The number $10$ is a commonly used number in number system especially in decimal system. Hence, he would like to split the quantities as multiplying factors on the basis of $10$. Thus, the logarithmic system is called as common logarithmic system.

Due to the use of $10$ in logarithms, Henry Briggs’s logarithmic system become most useful and successful than natural logarithmic system. Hence, it is also called as Henry Briggs’s logarithms.

Algebraic form

Logarithm is denoted by $\log$ symbol simply and $10$ is used as subscript of the log to say that $10$ is a base of the logarithm.

Representation

If a quantity is denoted by $q$, then logarithm of $q$ to base $10$ is written mathematically as $\log_{10}{q}$. It is also commonly written as $\log{q}$.

Therefore, $\log_{10}{q}$ and $\log{q}$ both represent common logarithm of quantity $q$ in mathematics.

Inverse Operation

The Common Logarithm and Exponentiation are inverse operations. So, it is essential to know the relation between them.

The total number of multiplying factors is denoted by $x$ when the quantity $q$ is divided as multiplying factors on the basis of another quantity $10$.

$\log_{10}{q} \,=\, x$ then $q \,=\, 10^{\displaystyle x}$

Therefore, $\log_{10}{q} \,=\, x$ $\, \Leftrightarrow \,$ $q \,=\, 10^{\displaystyle x}$

It can also be written as

$\log{q} \,=\, x$ $\, \Leftrightarrow \,$ $q \,=\, 10^{\displaystyle x}$