Linear equations in Two variables

An equation that represents a straight line in terms of two variables is called a linear equation in two variables.

Introduction

The mathematical equations are formed in terms of two variables in some cases. If the two variables have exponent one, then the mathematical equation represents a straight line geometrically. Therefore, an equation, which expressed in two variables is called the linear equation in two variables.

Example

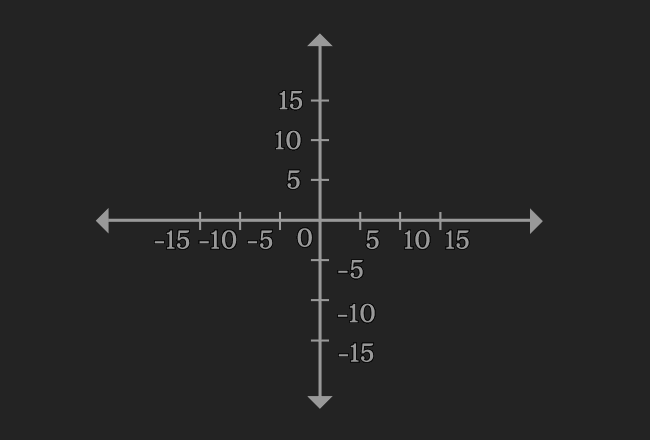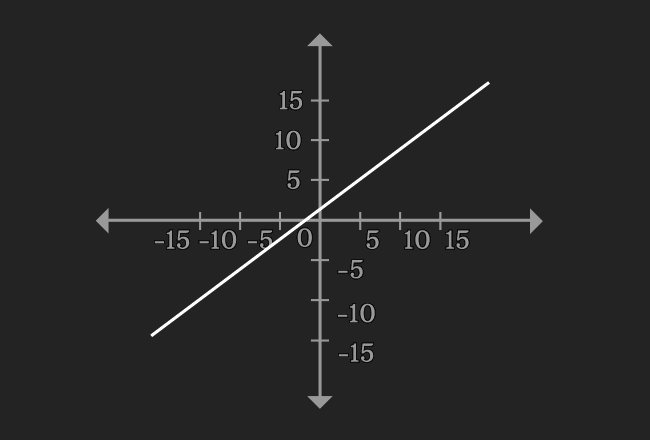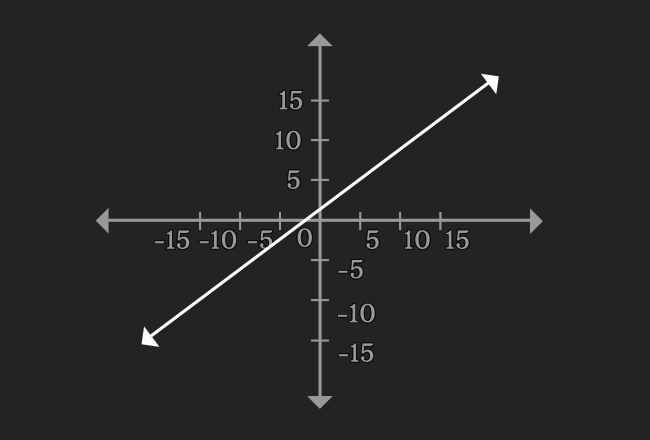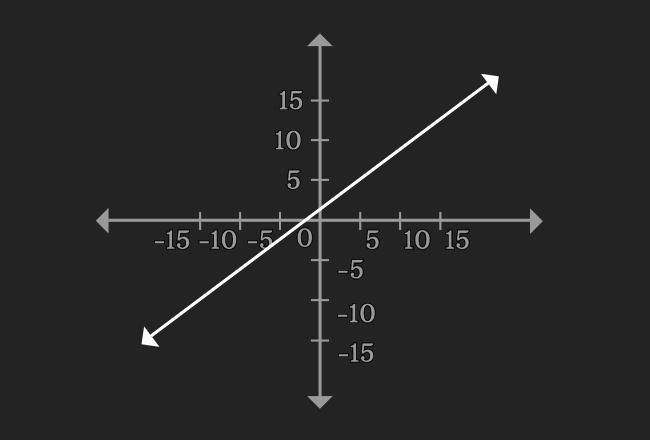
$3x-4y+5 = 0$
It is an equation, which expressed in terms of $x$ and $y$. Now, write any variable in terms of remaining variable.

$\implies$ $3x+5 = 4y$

$\implies$ $4y = 3x+5$

$\implies$ $y = \dfrac{3x+5}{4}$

Get values of $y$ by substituting different values in $x$, and then draw a graph by the values of $x$ and $y$.

You observe that the graph displays a straight line. It is mainly due to exponent one of both variables. Hence, the equation is called as a linear equation.

Examples

Here is some more examples for the linear equations in two variables.

1. $x-2y+6 = 0$
2. $-4p+4q = -3$
3. $7l-\sqrt{6}m-9 = 0$
4. $-0.6y+5z = 2$
5. $-8r-5s-4 = 0$

Algebraic form

$a$, $b$ and $c$ are constants, and $x$ and $y$ are variables. The linear equations in two variables can be written mathematically in two ways in algebraic form.

1. $ax+by+c = 0$
2. $ax+by = c$

Solving methods

There are three methods in mathematics to solve the simultaneous linear equations in two variables.

1. Substitution method
2. Elimination method
3. Cross multiplication method

Study each method with understandable solved problems to learn how to solve linear equations in two variables.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.