$\displaystyle \lim_{x \,\to\, 0} \dfrac{\sin{x}}{x}$ Rule

Formula

$\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sin{x}}{x}}$ $\,=\,$ $1$

In algebra, the letter $x$ is used to denote a variable and it is also used to represent an angle in radian in trigonometry. So, the sine of an angle $x$ is written as a trigonometric function $\sin{x}$ mathematically, where $x$ denotes an angle of a right triangle.

What is sinx/x Limit rule?

There is a mathematical relationship between trigonometric function $\sin{x}$ and angle $x$ and you should know that math property firstly to understand this trigonometric limit rule. Let’s learn it theoretically, when the value of angle $x$ is closer to zero, the quotient of $\sin{x}$ divided by $x$ is equal to one.

Look at the below graph and we can observe that the value of sine of angle $x$ divided by $x$ is equal to one, when the value of $x$ approaches to zero from left side.

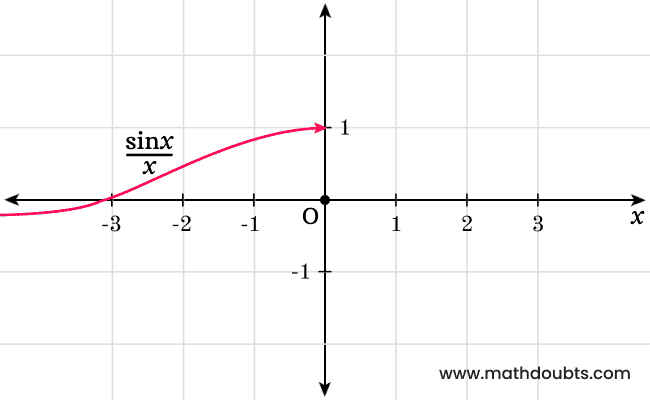
So, the left-sided limit of $\sin{x}$ over $x$ as $x$ tends to zero is equal to one and it is written mathematically in calculus as follows.

$\displaystyle \large \lim_{x \,\to\, 0^-}{\normalsize \dfrac{\sin{x}}{x}}$ $\,=\,$ $1$

Similarly, let’s observe the below graph and it clears that the value of sine of angle $x$ divided by $x$ is also equal to one, when the value of $x$ tends to zero from right side.

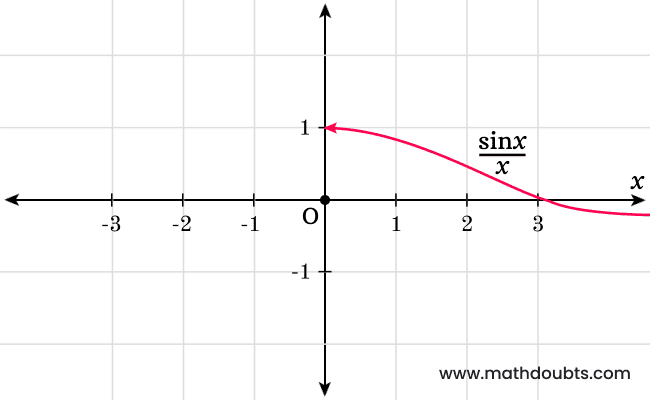
So, the right-sided limit of $\sin{x}/x$ as $x$ approaches to zero is also equal to one and it is written in mathematical form in calculus as follows.

$\displaystyle \large \lim_{x \,\to\, 0^+}{\normalsize \dfrac{\sin{x}}{x}}$ $\,=\,$ $1$

The above two cases visually clear that the limits of $\sin{x}$ divided by $x$ as the value of $x$ is closer to zero from both left and right sides are equal. So, the limit exists and it can be observed in the below graph.

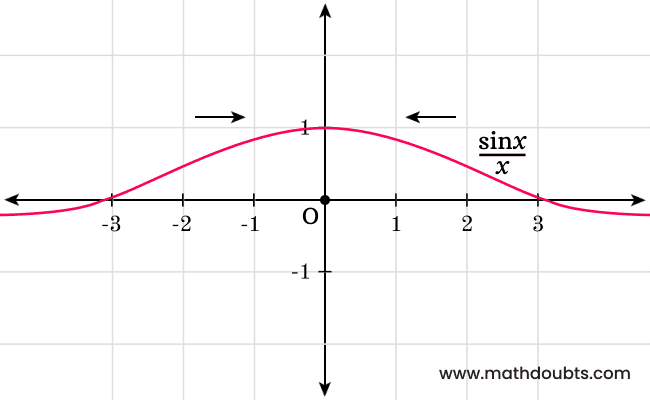
The equality property of trigonometric limits in sine can be expressed mathematically in calculus as follows.

$\displaystyle \large \lim_{x \,\to\, 0^-}{\normalsize \dfrac{\sin{x}}{x}}$ $\,=\,$ $1$ $\,=\,$ $\displaystyle \large \lim_{x \,\to\, 0^+}{\normalsize \dfrac{\sin{x}}{x}}$

The equality of the limits of both sides can be written in a standard limit form of trigonometric function as follows.

$\therefore\,\,\,\,\,\,$ $\displaystyle \large \lim_{x \,\to\, 0}{\normalsize \dfrac{\sin{x}}{x}}$ $\,=\,$ $1$

Therefore, the limit of $\sin{x}$ over $x$ as the value of $x$ approaches to zero is equal to one. It can be used as a formula in calculus to find the limits of trigonometric functions in which sine functions are involved.

This standard form of limits trigonometric rule is also written in the following form alternatively, where theta is used instead of $x$.

You have learned what the limit rule of $\sin{x}/x$ as $x$ approaches to zero. Now, let’s start learning how to prove the limit $x$ tends to zero $\sin{x}$ over $x$ formula in mathematics.

Proofs

There are two ways to prove this limit of trigonometric function property in mathematics.

Relation between Sine and Angle

It is derived on the basis of close relation between $\sin{x}$ function and angle $x$ as the angle $x$ closer to zero.

Taylor (or) Maclaurin Series Method

It can also be derived by the expansion of $\sin{x}$ function as per Taylor (or) Maclaurin series.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.