Identity Matrix

A matrix that consists of ones as diagonal elements and zeros as non-diagonal elements is called an identity matrix.

Introduction

In a special case, each element in the main diagonal (or leading diagonal) can be one and the remaining non-diagonal entries can be zeros in a matrix.

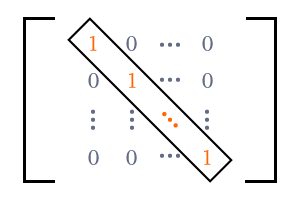
$I$ $\,=\,$ $\begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \color{red} \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ \end{bmatrix}$

There are two popular meanings for the word “identity” in English language.

1. Oneness
2. Unity

Hence, this type of matrix is called an identity matrix, and simply denoted by $I$ in mathematics. It is also called a unit matrix.

An identity matrix is basically a square matrix.

1. Diagonal elements are $1$s.
2. Non-diagonal elements are $0$s.

Due to these two reasons, a unit matrix is a diagonal matrix principally and also a scalar matrix.

Examples

The following three examples help you to understand how to express the identity matrices of different orders.

$I_2$ $\,=\,$
$\begin{bmatrix}
1 & 0 \\
0 & 1 \\
\end{bmatrix}
$

It is a matrix of the order $2 \times 2$ but it is an identity matrix and also a square matrix. Hence, it is known as an identity matrix of order $2$. It is simply denoted by $I_2$ in matrix.

$I_3$ $\,=\,$
$\begin{bmatrix}
1 & 0 & 0\\
0 & 1 & 0\\
0 & 0 & 1\\
\end{bmatrix}
$

It is a matrix of the order $3 \times 3$. It is an identity matrix and also a square matrix. Therefore, it is called an identity matrix of order $3$ and simply denoted by $I_3$ in mathematics.

$I_4$ $\,=\,$
$\begin{bmatrix}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0\\
0 & 0 & 1 & 0\\
0 & 0 & 0 & 1\\
\end{bmatrix}
$

It is a matrix of the order $4 \times 4$. It is an identity matrix and also a square matrix. So, it is called an identity matrix of order $4$ and simply denoted by $I_4$ in mathematics.

In this way, an identity matrix of any order can be expressed in mathematics.

$I_n$ $\,=\,$ $\begin{bmatrix} 1 & 0 & 0 & \cdots & 0 \\ 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ \vdots & \vdots & \vdots & \color{red} \ddots & \vdots \\ 0 & 0 & 0 & \cdots & 1 \\ \end{bmatrix}$

If the number of entries in each row is $n$ and the number of elements in each column is $n$, then it is called a matrix of the order $n \times n$. It is an identity matrix and also a square matrix. Hence, it is called an identity matrix of order $n$ and simply denoted by $I_n$ in mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.