Diagonal Matrix

A matrix that consists of zeros as entries (or elements) outside the main diagonal is called a diagonal matrix.

Introduction

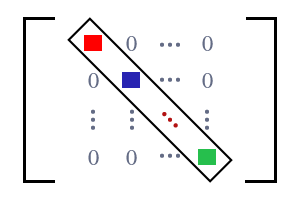
Square matrices are appeared with zeros. In a special case, a square matrix contains zero as non-diagonal elements but it contains elements only on principal diagonal. Due to having elements on leading diagonal and having zeros as non-diagonal elements, the square matrix is recognized as a diagonal matrix.

$M=\left[\begin{array}{ccccc}{e}_{1\⁣1}& 0& 0& \cdots & 0\\ 0& e_{2\⁣2}& 0& \cdots & 0\\ 0& 0& e_{3\⁣3}& \cdots & 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & e_{m\⁣m}\end{array}\right]$

The matrix is having elements $e_{1\⁣1},e_{2\⁣2},e_{3\⁣3},\dots e_{m\⁣m}$ only on principal diagonal but observe the elements on non-diagonal areas. All are zero elements at non-diagonal areas. Therefore, this type of matrix is called a diagonal matrix. The diagonal elements can be either equal or unequal elements.

It is simply expressed as $M=diag\left[\begin{array}{ccccc}{e}_{1\⁣1,}& e_{2\⁣2,}& e_{3\⁣3,}& \cdots & e_{n\⁣n}\end{array}\right]$

Example

$D$ is a square matrix of order $5\times 5$. It is having $25$ element in five rows and five columns.

$D=\left[\begin{array}{ccccc}1& 0& 0& 0& 0\\ 0& –5& 0& 0& 0\\ 0& 0& 7& 0& 0\\ 0& 0& 0& 3& 0\\ 0& 0& 0& 0& 9\end{array}\right]$

The matrix $D$ is having two types of elements. One type of elements are nonzero elements and remaining all are zeros. Nonzero elements ($1,–5,7,3$ and $9$) are placed on the leading diagonal and remaining non-diagonal elements are zeros. Therefore, the matrix $D$ is known as a diagonal matrix.

The diagonal matrix $D$ is written in simple form $D=diag\left[\begin{array}{ccccc}1,& –5,& 7,& 3,& 9\end{array}\right]$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.