The Hero’s or Heron’s formula can be derived in geometrical method by constructing a triangle by taking $a$, $b$, $c$ as lengths of the sides and $s$ as half of the perimeter of the triangle.
$\Delta PQR$ is a triangle. The lengths of sides of triangle $\overline{PQ}$, $\overline{QR}$ and $\overline{PR}$ are $a$, $b$ and $c$ respectively. The perimeter of the triangle is $a+b+c$ but it is denoted by $2s$ in heron’s formula.

Draw a perpendicular line to side $\overline{PR}$ from point $Q$ and it intersects the side $\overline{PR}$ at point $S$. Take, the length of the sides $\overline{QS}$ and $\overline{PS}$ are $h$ and $x$ respectively, then the length of the side $\overline{SR}$ is equal to $c-x$.
The $\Delta SPQ$ and $\Delta SRQ$ are two right triangles, which have $\overline{QS}$ as a common opposite side. Now, write the relation between sides of each triangle by the Pythagorean Theorem.
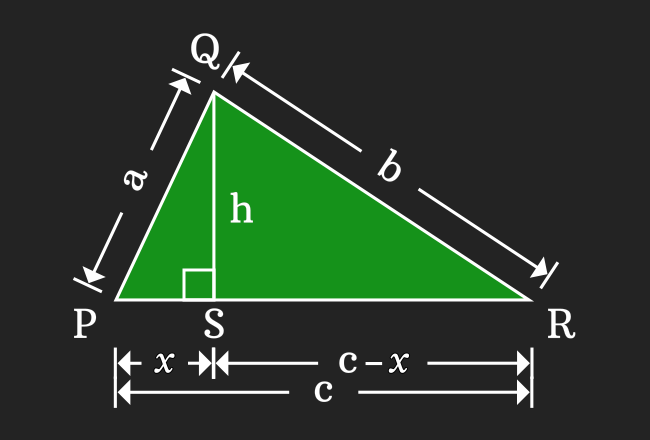
According to $\Delta SPQ$
$a^2 \,=\, x^2+h^2$
$\implies$ $h^2 \,=\, a^2-x^2$
According to $\Delta SRQ$
$b^2 \,=\, (c-x)^2+h^2$
$\implies$ $h^2 \,=\, b^2-(c-x)^2$
Now, replace the $h^2$ by its equivalent value as per right triangle $SPQ$. Then, simplify the algebraic expression to find the value of the $x$.
$\implies$ $a^2-x^2$ $\,=\,$ $b^2-(c-x)^2$
$\implies$ $a^2-x^2$ $\,=\,$ $b^2-(c^2+x^2-2cx)$
$\implies$ $a^2-x^2$ $\,=\,$ $b^2-c^2-x^2+2cx$
$\implies$ $a^2-b^2+c^2$ $\,=\,$ $x^2-x^2+2cx$
$\implies$ $\require{cancel} a^2-b^2+c^2$ $\,=\,$ $\cancel{x^2}-\cancel{x^2}+2cx$
$\implies$ $a^2-b^2+c^2 \,=\, 2cx$
$\implies$ $2cx \,=\, a^2-b^2+c^2$
$\,\,\, \therefore \,\,\,\,\,\,$ $x \,=\, \dfrac{a^2-b^2+c^2}{2c}$
In PQR, the base of the triangle is PR and it is equal to c but the height of the triangle is unknown. For calculating the area of a triangle, it is required to know both base and height of triangle. So, let us evaluate the height of the triangle from the following equation, which was derived in previous step from the $\Delta SPQ$.
$h^2 \,=\, a^2-x^2$
Now, substitute the value of $x$ in this equation to find the height of the triangle.
$\implies$ $h^2$ $\,=\,$ $a^2-\Bigg(\dfrac{a^2-b^2+c^2}{2c}\Bigg)^2$
$\implies$ $h^2$ $\,=\,$ $\Bigg(a+\dfrac{a^2-b^2+c^2}{2c}\Bigg)$ $\Bigg(a-\dfrac{a^2-b^2+c^2}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{a\times 2c + (a^2-b^2+c^2)}{2c}\Bigg)$ $\Bigg(\dfrac{a\times 2c -(a^2-b^2+c^2)}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{2ac+a^2-b^2+c^2}{2c}\Bigg)$ $\Bigg(\dfrac{2ac-a^2+b^2-c^2}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{a^2+c^2+2ac-b^2}{2c}\Bigg)$ $\Bigg(\dfrac{-a^2-c^2+2ac+b^2}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{a^2+c^2+2ac-b^2}{2c}\Bigg)$ $\Bigg(\dfrac{-(a^2+c^2-2ac)+b^2}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{(a+c)^2-b^2}{2c}\Bigg)$ $\Bigg(\dfrac{-(a-c)^2+b^2}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{(a+c)^2-b^2}{2c}\Bigg)$ $\Bigg(\dfrac{b^2-(a-c)^2}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{(a+c+b)(a+c-b)}{2c}\Bigg)$ $\Bigg(\dfrac{(b+(a-c))(b-(a-c))}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{(a+b+c)(a+c-b)}{2c}\Bigg)$ $\Bigg(\dfrac{(b+a-c)(b-a+c)}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{(a+b+c)(a+c-b)}{2c}\Bigg)$ $\Bigg(\dfrac{(a+b-c)(-a+b+c)}{2c}\Bigg)$
Now, express the each factor in terms of perimeter.
Now, simplify this algebraic expression by substituting the equivalent value of every factor.
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{(2s)(2(s-b))}{2c}\Bigg)$ $\Bigg(\dfrac{(2(s-c))(2(s-a))}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{2s \times 2(s-b)}{2c}\Bigg)$ $\Bigg(\dfrac{2(s-c) \times 2(s-a)}{2c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{2 \times s \times 2(s-b)}{2 \times c}\Bigg)$ $\Bigg(\dfrac{2 \times (s-c) \times 2(s-a)}{2 \times c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\require{cancel} \Bigg(\dfrac{\cancel{2} \times s \times 2(s-b)}{\cancel{2} \times c}\Bigg)$ $\Bigg(\dfrac{\cancel{2} \times (s-c) \times 2(s-a)}{\cancel{2} \times c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\Bigg(\dfrac{2s(s-b)}{c}\Bigg)\Bigg(\dfrac{2(s-a)(s-c)}{c}\Bigg)$
$\implies$ $h^2$ $\,=\,$ $\dfrac{2s(s-b) \times 2(s-a)(s-c)}{c \times c}$
$\implies$ $h^2$ $\,=\,$ $\dfrac{4s(s-a)(s-b)(s-c)}{c^2}$
$\implies$ $h$ $\,=\,$ $\pm \sqrt{\dfrac{4s(s-a)(s-b)(s-c)}{c^2}}$
According to Physics, the height is a positive factor. So, just consider positive value as the height in this case.
$\implies$ $h$ $\,=\,$ $\sqrt{\dfrac{4s(s-a)(s-b)(s-c)}{c^2}}$
$\implies$ $h$ $\,=\,$ $\sqrt{\dfrac{4}{c^2} \times s(s-a)(s-b)(s-c)}$
$\implies$ $h \,=\, \sqrt{\dfrac{2^2}{c^2} \times s(s-a)(s-b)(s-c)}$
$\implies$ $h \,=\, \sqrt{\Big(\dfrac{2}{c}\Big)^2 \times s(s-a)(s-b)(s-c)}$
$\implies$ $h \,=\, \sqrt{\Big(\dfrac{2}{c}\Big)^2} \times \sqrt{s(s-a)(s-b)(s-c)}$
$\implies$ $h \,=\, \dfrac{2}{c} \times \sqrt{s(s-a)(s-b)(s-c)}$
Now, use the cross multiplication for bringing the factor $\dfrac{2}{c}$ to left hand side of the equation.

$\implies$ $c \times h \,=\, 2 \times \sqrt{s(s-a)(s-b)(s-c)}$
$\implies$ $\dfrac{c \times h}{2} \,=\, \sqrt{s(s-a)(s-b)(s-c)}$
$\implies$ $\dfrac{1 \times c \times h}{2} \,=\, \sqrt{s(s-a)(s-b)(s-c)}$
$\implies$ $\dfrac{1}{2} \times c \times h \,=\, \sqrt{s(s-a)(s-b)(s-c)}$
According to Geometry, the half of the product of base and height of the triangle is the area of the respective triangle.
$\,\,\, \therefore \,\,\,\,\,\,$ $A \,=\, \sqrt{s(s-a)(s-b)(s-c)}$
Thus, a mathematician Hero of Alexandria derived the area of a triangle in mathematics. It is denoted by either $A$ or $\Delta$ in mathematics. It is called as Heron’s formula or Hero’s formula.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved