Evaluate $\dfrac{\sin{x}-\tan{x}\cos^2{x}}{\cos{x}-1+\sin^2{x}}$

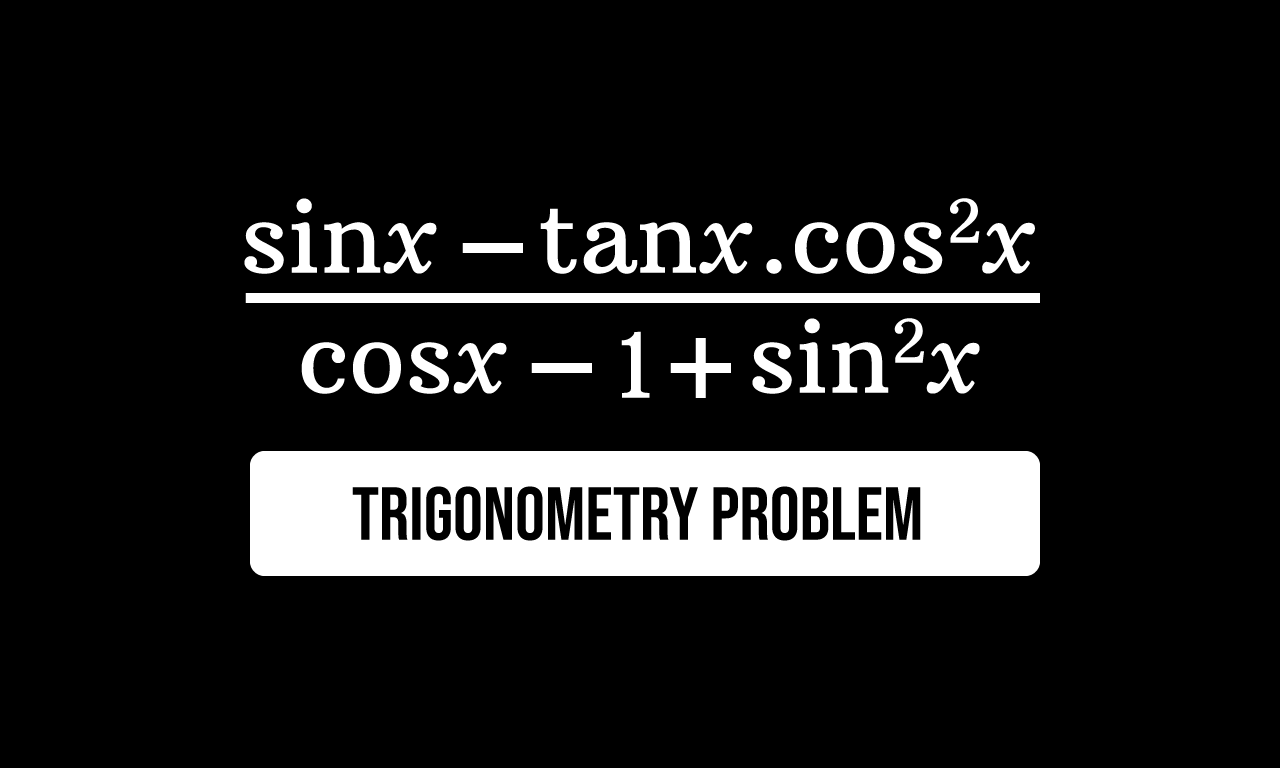
The sine of angle $x$ minus the product of tan of angle $x$ and cos squared of $x$ divided by the cosine of angle $x$ minus one plus square of sine of angle $x$ is a given rational function in terms of trigonometric ratios in this trigonometry problem.

$\dfrac{\sin{x}-\tan{x}\cos^2{x}}{\cos{x}-1+\sin^2{x}}$

The above trigonometric function in rational form represents a value and it can be evaluated by simplifying it by the trigonometric identities.

Simplify the Expression in Numerator

Firstly, let us try to simplify the trigonometric expression in the numerator.

$=\,\,\,$ $\dfrac{\sin{x}-\tan{x} \times \cos^2{x}}{\cos{x}-1+\sin^2{x}}$

The tan of angle $x$ can be expressed as a quotient of the sine of angle $x$ divided by the cosine of angle $x$ as per the quotient rule of sine and cosine of angles.

$=\,\,\,$ $\dfrac{\sin{x}-\dfrac{\sin{x}}{\cos{x}} \times \cos^2{x}}{\cos{x}-1+\sin^2{x}}$

The second term is a product of two fractions $\sin{x}$ divided by $\cos{x}$ and square of $\cos{x}$. It can be calculated by the multiplication rule of fractions.

$=\,\,\,$ $\dfrac{\sin{x}-\dfrac{\sin{x} \times \cos^2{x}}{\cos{x}}}{\cos{x}-1+\sin^2{x}}$

$=\,\,\,$ $\dfrac{\sin{x}-\dfrac{\sin{x} \times \cancel{\cos^2{x}}}{\cancel{\cos{x}}}}{\cos{x}-1+\sin^2{x}}$

$=\,\,\,$ $\dfrac{\sin{x}-\sin{x} \times \cos{x}}{\cos{x}-1+\sin^2{x}}$

$=\,\,\,$ $\dfrac{\sin{x} \times 1-\sin{x} \times \cos{x}}{\cos{x}-1+\sin^2{x}}$

In the numerator, $\sin{x}$ is a common factor in the both terms. So, it can be taken out common from them to factorize (or fractorise) the expression.

$=\,\,\,$ $\dfrac{\sin{x} \times (1-\cos{x})}{\cos{x}-1+\sin^2{x}}$

Simplify the expression in Denominator

It is time to concentrate on the expression in the denominator. The first term is a term in cos function and third term is a term in the sine function. The cosine function cannot be converted but the the square of sine function can be converted into cos function as per the sine squared identity.

$=\,\,\,$ $\dfrac{\sin{x} \times (1-\cos{x})}{\cos{x}-1+1-\cos^2{x}}$

Now, simplify the trigonometric expression in the denominator for this rational expression.

$=\,\,\,$ $\dfrac{\sin{x} \times (1-\cos{x})}{\cos{x}-\cancel{1}+\cancel{1}-\cos^2{x}}$

$=\,\,\,$ $\dfrac{\sin{x} \times (1-\cos{x})}{\cos{x}-\cos^2{x}}$

In the denominator, $\cos{x}$ is a common factor in both terms. So, let’s take the factor $\cos{x}$ common from the two terms of the trigonometric expression.

$=\,\,\,$ $\dfrac{\sin{x} \times (1-\cos{x})}{\cos{x} \times 1-\cos^2{x}}$

$=\,\,\,$ $\dfrac{\sin{x} \times (1-\cos{x})}{\cos{x} \times (1-\cos{x})}$

Evaluate the Expression by simplification

It is a time to simplify the whole rational function. One minus cosine of angle $x$ is a factor in both numerator and denominator. So, they both get cancelled each other as per the division rule of equal quantities.

$=\,\,\,$ $\dfrac{\sin{x} \times \cancel{(1-\cos{x})}}{\cos{x} \times \cancel{(1-\cos{x})}}$

$=\,\,\,$ $\dfrac{\sin{x}}{\cos{x}}$

According to the quotient of sine divided by cosine rule, the quotient of sine of angle $x$ divided by cosine of angle $x$ is equal to tan of angle $x$.

$=\,\,\,$ $\tan{x}$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.