The cos double angle identity is a mathematical formula in trigonometry and used to expand cos functions which contain double angle. For example, if theta ($\theta$) is angle of a right triangle, then the cos of double angle is written as $\cos{(2θ)}$. It is expanded mathematically as follows.
$\cos{(2\theta)}$ $\,=\,$ $\cos^2{\theta}-\sin^2{\theta}$
It is your time to know how cos of double angle formula is derived in mathematical form in trigonometry by geometry.
The cos of double angle identity can be derived in trigonometry by constructing a right triangle with double angle. Follow the below steps to get the requisite triangle.
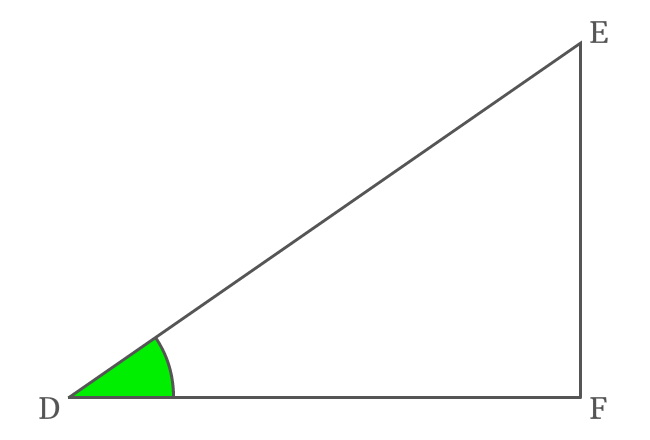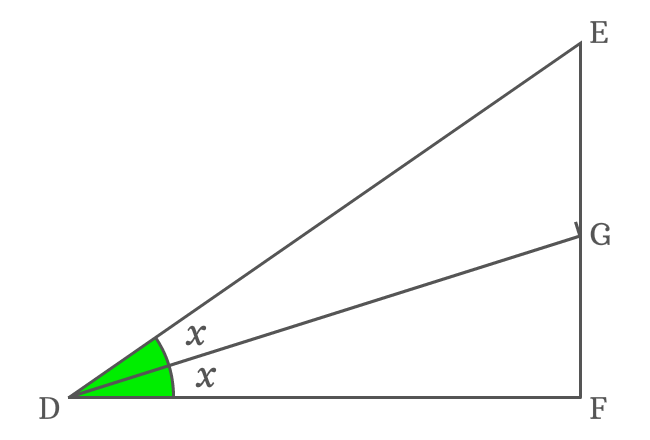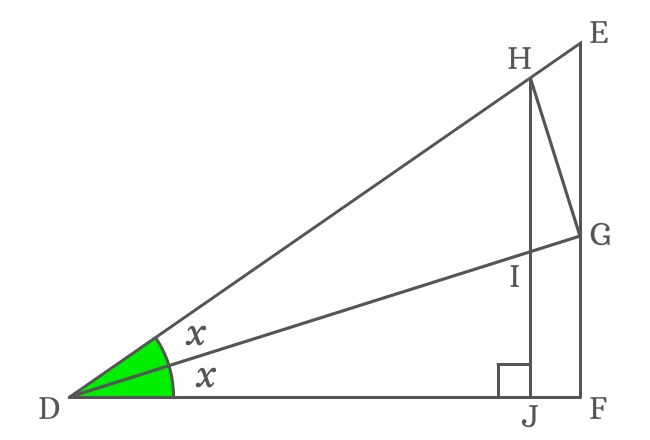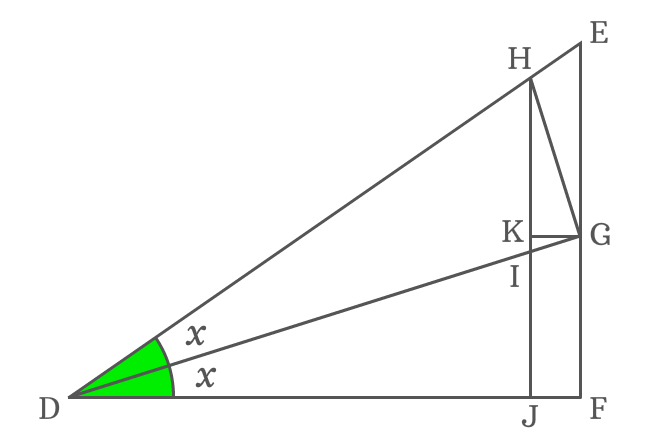
A right triangle is constructed geometrically with double angle and it is used to find the expansion of cos double angle function in trigonometric form mathematically.
The angle of $\Delta FDE$ is $2x$ and it is double angle. Geometrically, $\Delta FDE$ and $\Delta JDH$ are similar triangles. So, the angle of $\Delta JDH$ is also $2x$.
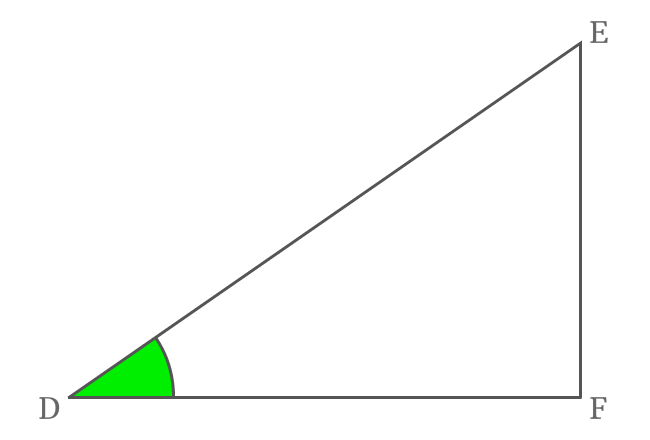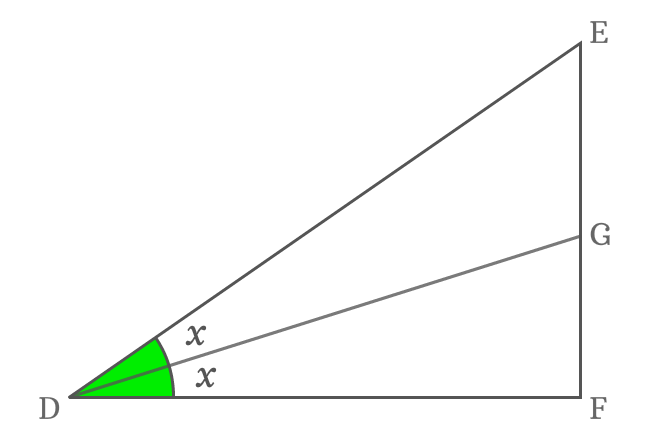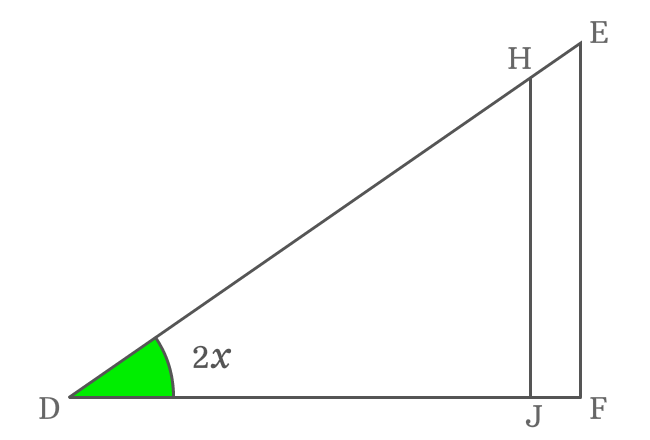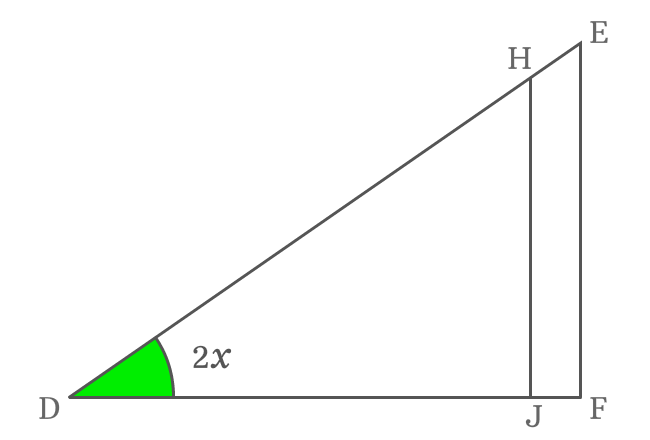
According to $\Delta JDH$, write cos of double angle in its ratio form. $\overline{DJ}$ is adjacent side (base) and $\overline{DH}$ is hypotenuse in this triangle.
$\cos{2x} = \dfrac{DJ}{DH}$
Actually, the side $\overline{HJ}$ divides the side $\overline{DF}$ as two sides $\overline{DJ}$ and $\overline{JF}$.
$DF \,=\, DJ + JF$
$\implies DJ = DF \,–\, JF$
Therefore, the length of side $\overline{DJ}$ can be written as the subtraction of lengths of side $\overline{DF}$ from side $\overline{JF}$.
$\implies \cos{2x}$ $\,=\,$ $\dfrac{DF-JF}{DH}$
$\implies \cos{2x}$ $\,=\,$ $\dfrac{DF}{DH}-\dfrac{JF}{DH}$
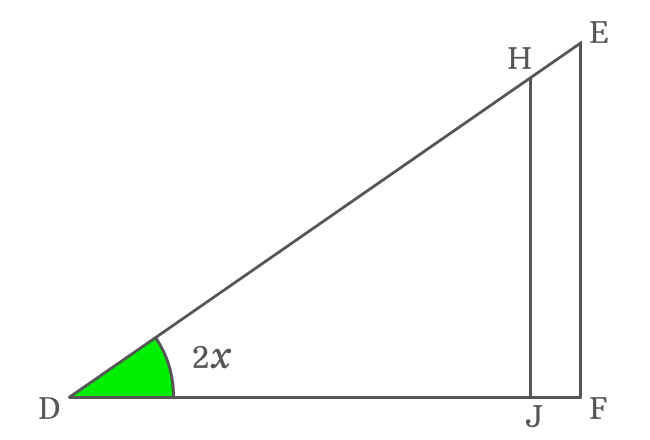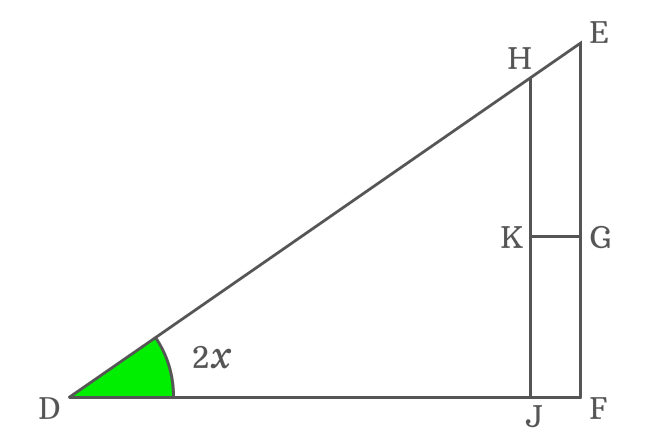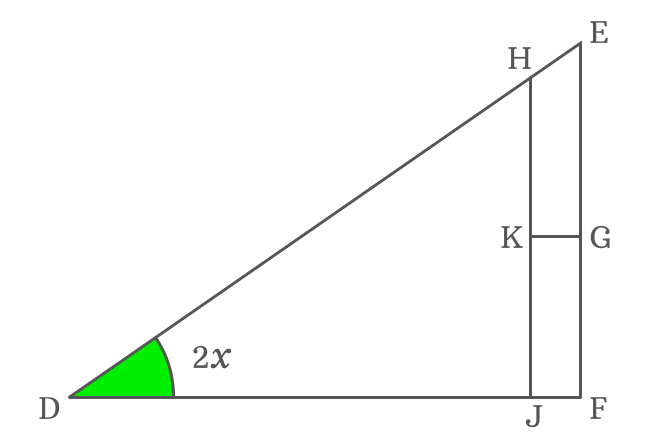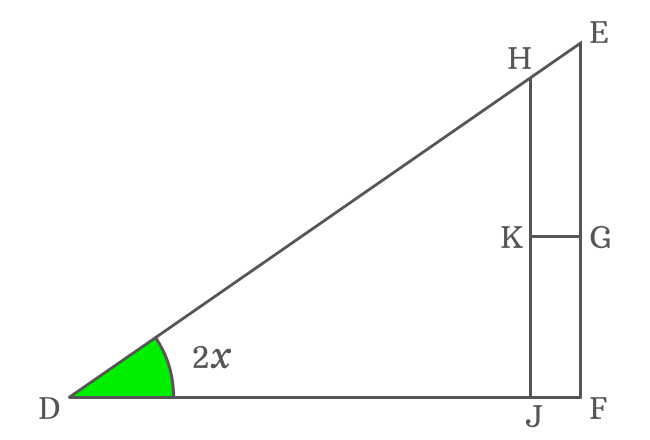
The side $\overline{KG}$ is parallel to the side $\overline{JF}$. Similarly, the sides $\overline{HJ}$ and $\overline{EF}$ are also parallel lines. Hence, the lengths of sides $\overline{KG}$ and $\overline{JF}$ are equal geometrically.
$JF = KG$
Therefore, the length of the side $\overline{JF}$ can be replaced by the length of the side $\overline{KG}$ in the expansion of $\cos{(2x)}$ function.
$\implies \cos{2x}$ $\,=\,$ $\dfrac{DF}{DH}-\dfrac{KG}{DH}$
The cos double angle function is expanded in terms of sides. So, it is time to transform them into trigonometric functions.
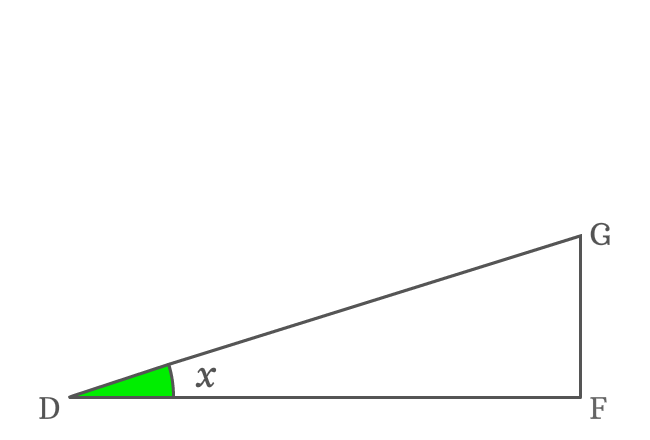
$\overline{DF}$ is adjacent side of $\Delta FDG$ and its angle is $x$. The relation between them can be written in the following way.
$\cos{x} \,=\, \dfrac{DF}{DG}$
$\implies DF = {DG}\cos{x}$
Substitute the length of the side $\overline{DF}$ by its equal value in the $\cos{2x}$ expansion.
$\implies \cos{2x}$ $\,=\,$ $\dfrac{{DG}\cos{x}}{DH}-\dfrac{KG}{DH}$
$\implies \cos{2x}$ $\,=\,$ $\dfrac{DG}{DH} \times \cos{x}$ $-$ $\dfrac{KG}{DH}$
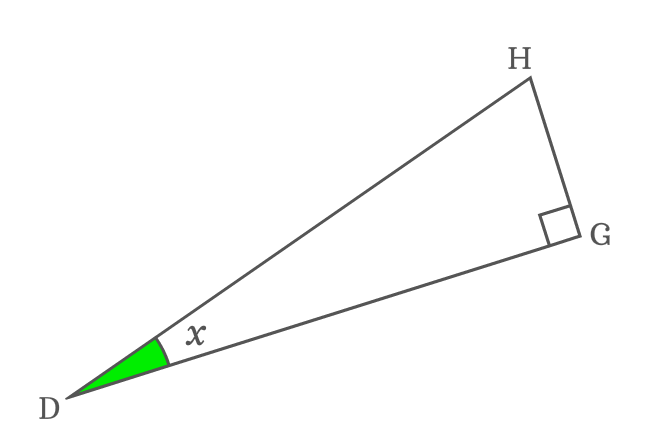
$\overline{DG}$ and $\overline{DH}$ are adjacent side and hypotenuse of $\Delta GDH$. The ratio of them can be represented by cosine function.
$\cos{x} \,=\, \dfrac{DG}{DH}$
Now, replace the ratio between the lengths of sides $\overline{DG}$ and $\overline{DH}$ in the cos double angle expansion.
$\implies \cos{2x}$ $\,=\,$ $\cos{x} \times \cos{x}-\dfrac{KG}{DH}$
$\implies \cos{2x}$ $\,=\,$ $\cos^2{x}-\dfrac{KG}{DH}$
In the same way, let’s try to transform the remaining ratio in trigonometric form.
$\overline{KG}$ is a side of $\Delta KHG$ but angle of this right triangle is unknown. So, it is not possible to continue the derivation of $\cos{(2x)}$ expansion further until this obstacle is overcome.
$\overline{KG}$ and $\overline{DF}$ are two parallel lines and $\overline{DG}$ is their transversal. The $\angle FDG$ and $\angle KGD$ are alternate interior angles and they are equal geometrically but $\angle GDF$ is $x$.
$\angle KGD = \angle GDF = x$
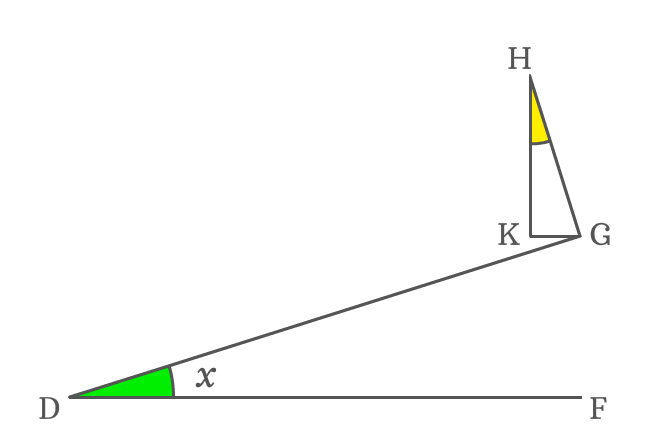
The side $\overline{HG}$ is a perpendicular line to side $\overline{DG}$. So, the angle between them is a right angle but the side $\overline{KG}$ splits it as $\angle HGK$ and $\angle KGD$.
$\angle HGK + \angle KGD = 90^°$
$\implies \angle HGK = 90^° – \angle KGD$
$\implies \angle HGK = 90^° – x$
In $\Delta KHG$, the $\angle KHG$ is unknown but the remaining two angles are known. It can be evaluated by the sum of angles of a triangle rule .
$\angle KHG + \angle HKG + \angle KGH$ $\,=\,$ $180^°$
$\implies$ $\angle KHG + 90^° + 90^°-x$ $\,=\,$ $180^°$
$\implies$ $\angle KHG + 180^°-x$ $\,=\,$ $180^°$
$\implies$ $\angle KHG$ $\,=\,$ $180^°-180^°+x$
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle KHG \,=\, x$
Therefore, it is derived that the angle of $\Delta KHG$ is also $x$ because it is a similar triangle. Now, the derivation of $\cos{(2x)}$ identity can be continued further.
$\overline{KG}$ is opposite side of $\Delta KHG$ and it is determined that the angle of this triangle is $x$. Now, express relation between them in trigonometric form.
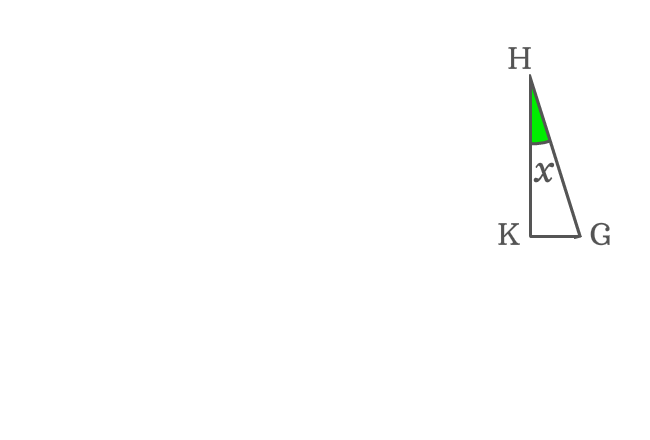
$\sin{x} \,=\, \dfrac{KG}{HG}$
$\implies KG \,=\, {HG}\sin{x}$
Now, substitute the length of the side $\overline{KG}$ by its equivalent value in the $\cos{2x}$ expansion.
$\implies \cos{2x}$ $\,=\,$ $\cos^2{x}-\dfrac{{HG}\sin{x}}{DH}$
$\implies \cos{2x}$ $\,=\,$ $\cos^2{x}-\dfrac{{HG}}{DH} \times \sin{x}$
$\overline{HG}$ is opposite side and $\overline{DH}$ is hypotenuse of right triangle $GDH$. Consider this triangle one more time.

In $\Delta GDH$, the angle of this triangle is $x$ and the ratio of lengths of opposite side to hypotenuse is $\sin{x}$.
$\sin{x} \,=\, \dfrac{HG}{DH}$
Now, replace the ratio of lengths of sides $\overline{HG}$ to $\overline{DH}$ by $\sin{x}$ in the $\cos{2x}$ expansion.
$\implies \cos{2x}$ $\,=\,$ $\cos^2{x}-\sin{x} \times \sin{x}$
$\,\,\, \therefore \,\,\,\,\,\, \cos{2x}$ $\,=\,$ $\cos^2{x}-\sin^2{x}$
Therefore, it is proved that the expansion of cos double angle function is equal to subtraction of squares of sin of angle from cos of angle. It is called as cos double angle identity and used as a formula in trigonometry.
The cos double angle identity is used to expand any cosine function which contains double angle.
$(1) \,\,\,\,\,\,$ $\cos{(2A)}$ $\,=\,$ $\cos^2{A}-\sin^2{A}$
$(2) \,\,\,\,\,\,$ $\cos{(2\alpha)}$ $\,=\,$ $\cos^2{\alpha}-\sin^2{\alpha}$
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved