$\cos{(30^°)}$ Proof

The cos of 30 degrees value can be derived mathematically in three methods. One of them is a trigonometric approach and other two are geometrical methods.

Theoretical approach

You must know the direct relation between the sides of a right triangle when its angle is $30$ degrees. According to properties of right triangle, the length of opposite side is half of the length of hypotenuse if the angle of right triangle is $\dfrac{\pi}{6}$. The exact value of $\cos{(30^°)}$ is evaluated theoretically on the basis of this property.

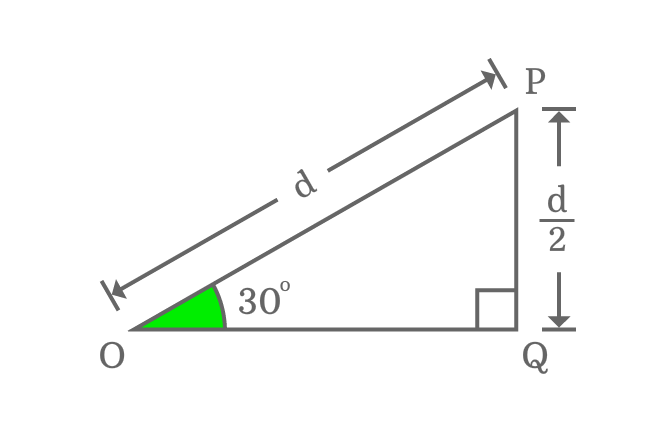
The lengths of opposite side and hypotenuse are known but the length of adjacent side is unknown in this case. It is essential to find it in order to find the $\cos{\Big(\dfrac{\pi}{6}\Big)}$ value. So, try Pythagorean Theorem to find the value of adjacent side mathematically.

${OP}^2 \,=\, {PQ}^2+{OQ}^2$

In $\Delta QOP$, the lengths of hypotenuse and opposite sides are $d$ and $\dfrac{d}{2}$ respectively.

$\implies d^2 = {\Big(\dfrac{d}{2}\Big)}^2+{OQ}^2$

$\implies d^2 = \dfrac{d^2}{4}+{OQ}^2$

$\implies d^2-\dfrac{d^2}{4} = {OQ}^2$

$\implies {OQ}^2 = d^2-\dfrac{d^2}{4}$

$\implies {OQ}^2 = d^2{\Bigg(1-\dfrac{1}{4}\Bigg)}$

$\implies {OQ}^2 = d^2{\Bigg(\dfrac{1 \times 4 -1}{4}\Bigg)}$

$\implies {OQ}^2 = d^2{\Bigg(\dfrac{4-1}{4}\Bigg)}$

$\implies {OQ}^2 = d^2{\Bigg(\dfrac{3}{4}\Bigg)}$

$\implies OQ = \sqrt{\dfrac{3d^2}{4}}$

$\implies OQ = \dfrac{\sqrt{3}d}{2}$

$\implies \dfrac{OQ}{d} = \dfrac{\sqrt{3}}{2}$

In this case, $d$ represents the length of hypotenuse $(OP)$.

$\implies \dfrac{OQ}{OP} = \dfrac{\sqrt{3}}{2}$

$\implies \dfrac{Length \, of \, Adjacent \, side}{Length \, of \, Hypotenuse} = \dfrac{\sqrt{3}}{2}$

The angle of $\Delta QOP$ is $\dfrac{\pi}{6}$ and the ratio represents $\cos{(30^°)}$ as per definition of trigonometric ratio cosine.

$\therefore \,\,\, \cos{(30^°)} = \dfrac{\sqrt{3}}{2}$

Therefore, it is derived that the exact value of cos of $30$ degrees in fraction form is $\dfrac{\sqrt{3}}{2}$ and its value in decimal form is $0.8660254037\ldots$

$\cos{(30^°)} = \dfrac{\sqrt{3}}{2} = 0.8660254037\ldots$

Practical approach

The value of cosine of $\dfrac{\pi}{6}$ can be calculated geometrically by constructing a right triangle with $30$ degrees angle using geometric tools.

1. Identify a point $G$ on the plane and then draw a straight line from this point horizontally.
2. Take protractor and coincide its centre with point $G$ and also coincide its right side base line with horizontal line. Now, mark a point at $30$ degrees.
3. Draw a line from point $G$ through $30$ degrees angle line by a ruler.
4. Draw an arc on $30$ degrees line from point $G$ by compass with any length. For example $7.5 \, cm$. The arc cuts the $30^°$ line at point $H$.
5. Draw a perpendicular line to horizontal line from point $H$ and it intersects the horizontal line at point $I$.

The five geometrical steps have constructed a right triangle, called as $\Delta HGI$ with an angle of $30$ degrees. The value of $\cos{\Big(\dfrac{\pi}{6}\Big)}$ can be calculated from this triangle mathematically.

$\cos{(30^°)} = \dfrac{Length \, of \, Adjacent \, side}{Length \, of \, Hypotenuse}$

$\implies \cos{(30^°)} \,=\, \dfrac{GI}{GH}$

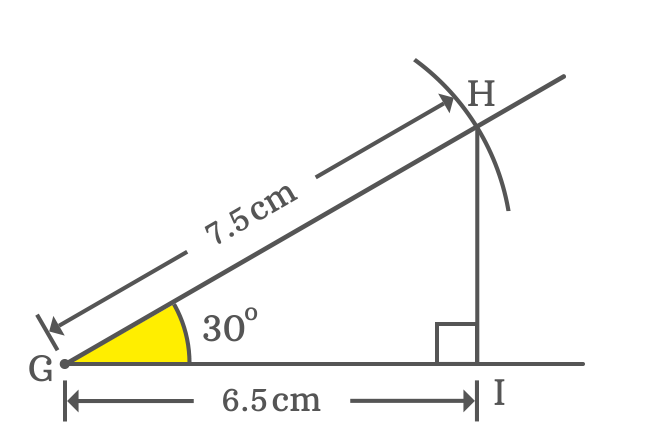
In this example, it is taken that the length of hypotenuse is $7.5 \, cm$ but the length of adjacent side is unknown. However, it can be measured by a ruler.

Now, measure the length of the adjacent side by ruler and you will observe that its length is $6.5 \, cm$ approximately. Now, calculate the value of $\cos{\Big({33\dfrac{1}{3}}^g\Big)}$

$\implies \cos{(30^°)} \,=\, \dfrac{GI}{GH} = \dfrac{6.5}{7.5}$

$\,\,\, \therefore \,\,\,\,\,\, \cos{(30^°)} \,=\, 0.8666666666\ldots$

Trigonometric approach

The $\cos{\Bigg({33\dfrac{1}{3}}^g\Bigg)}$ value is evaluated exactly in trigonometry by the cos squared identity. The exact value of $\cos{\Big(\dfrac{\pi}{6}\Big)}$ is actually calculated by substituting the value of sin 30 degrees in this formula.

$\cos{(30^°)} \,=\, \sqrt{1-\sin^2{(30^°)}}$

$\implies \cos{(30^°)} \,=\, \sqrt{1-{\Bigg(\dfrac{1}{2}\Bigg)}^2}$

$\implies \cos{(30^°)} \,=\, \sqrt{1-\dfrac{1}{4}}$

$\implies \cos{(30^°)} \,=\, \sqrt{\dfrac{1 \times 4 -1}{4}}$

$\implies \cos{(30^°)} \,=\, \sqrt{\dfrac{4-1}{4}}$

$\implies \cos{(30^°)} \,=\, \sqrt{\dfrac{3}{4}}$

$\implies \cos{(30^°)} \,=\, \dfrac{\sqrt{3}}{2}$

$\,\,\, \therefore \,\,\,\,\,\, \cos{(30^°)} \,=\, \dfrac{\sqrt{3}}{2}$

Verdict

According to both theoretical geometric and trigonometric methods, it is proved that the $\cos{\Big(\dfrac{\pi}{6}\Big)}$ value is $\dfrac{\sqrt{3}}{2}$ and its approximate value is $0.8660254037\ldots$

It is also evaluated that the value of $\cos{(30^°)}$ in practical geometrical method is $0.8666666666\ldots$ Now, compare both values of $\cos{(30^°)}$ and you observe that the value of $\cos{(30^°)}$ slightly differs with the value obtained from theoretical and trigonometric approaches. It is due to measuring the length of adjacent side approximately. However, the approximate values of $\cos{\Big(\dfrac{\pi}{6}\Big)}$ are same.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.