Proof for Cosine of 18 degrees in Geometric method

You have learned how to derive the value of cos 18 degrees in trigonometric method. It is time to learn how to derive the value of cosine of angle eighteen degree experimentally in geometric method. It is practically possible by constructing a right triangle (or right angled triangle) with an angle of eighteen degrees.

1. Use a ruler and draw a line of any length horizontally. For example, $10 \, cm$ line is drawn and it is called the line $\overline{DE}$.
2. Use a protractor and draw a perpendicular line to the line segment $\overline{DE}$ at point $E$.
3. Now, coincide the middle point of the protractor with the point $D$, then mark on plane at $18$ degrees indication line of protractor in anticlockwise direction. Finally, draw a line from point $D$ through $18$ degrees mark and it intersects the perpendicular line at point $F$.

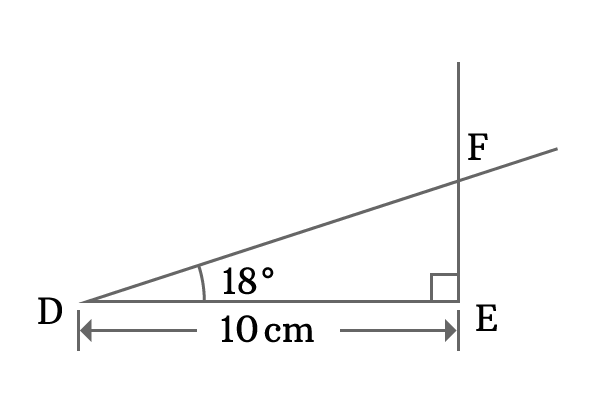
The three steps helped us in constructing a right triangle, known as $\Delta FDE$. In this case, the angle of the right angled triangle is $18$ degrees. So, let us evaluate the cosine of angle $\dfrac{\pi}{10}$ radian.

$\cos{(18^\circ)} \,=\, \dfrac{DE}{DF}$

The length of the adjacent side ($\overline{DE}$) is $10 \, cm$ but the length of the hypotenuse ($\overline{DF}$) is unknown. However, it can be measured by using a ruler and it is measured that the length of the hypotenuse is $10.5 \, cm$.

$\implies$ $\cos{(18^\circ)} \,=\, \dfrac{10}{10.5}$

$\implies$ $\cos{(18^\circ)} \,=\, 0.9523809523\ldots$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.