Completing the square

A mathematical approach of converting a quadratic expression into the square of the sum or difference of the terms is called completing the square.

Introduction

The quadratic expressions often appear in mathematics. Each quadratic expression is equal to zero for two values and they are called zeros or roots. There is a fundamental technique to find the zeros or roots of the quadratic polynomials.

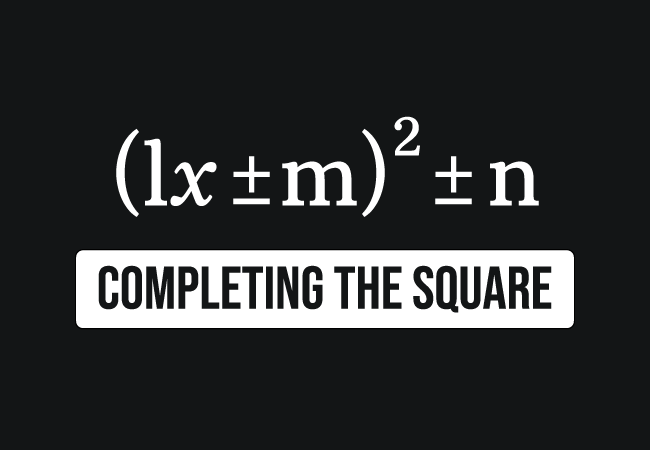
A quadratic expression is basically a second degree polynomial. So, it is possible to convert the whole polynomial into the square form of the sum or difference of the terms. Hence, this mathematical approach is called completing the square method.

$ax^2+bx+c$

A quadratic polynomial is generally written in the above mathematical form. The square of sum of square of difference algebraic identities can be used to convert this standard form expression in the form of either square of sum or square of difference of the terms as follows.

$\implies$ $ax^2+bx+c$ $\,=\,$ $(lx \pm m)^2 \pm n$

The method of this conversion is called completing the square. It may confuse you initially but the following examples help you to understand it easily.

Examples

$(1).\,\,\,$ $x^2+6x+4$

In the given polynomial, the sign of second term is positive. So, it can be converted in the form of the square of sum of two terms by the square of sum of two terms rule.

$=\,\,\,$ $x^2+2 \times 3x+4$

$=\,\,\,$ $x^2+2 \times 3 \times x+4$

$=\,\,\,$ $x^2+2 \times x \times 3+4$

Now, add $3$ squared to the expression and subtract the same quantity from the polynomial.

$=\,\,\,$ $x^2+2 \times x \times 3+3^2-3^2+4$

$=\,\,\,$ $(x^2+2 \times x \times 3+3^2)-3^2+4$

$=\,\,\,$ $(x^2+3^2+2 \times x \times 3)-9+4$

$=\,\,\,$ $(x+3)^2-5$

$\therefore\,\,\,$ $x^2+6x+4$ $\,=\,$ $(x+3)^2-5$

Therefore, the given quadratic polynomial $x^2+6x+4$ is successfully converted as $(x+3)^2-5$.

$(2).\,\,\,$ $4x^2-20x+21$

The sign of the second term in the above algebraic expression is negative. Hence, it can be transformed in the form of the square of the difference of the two terms by the square of difference of two terms identity.

$=\,\,\,$ $(2x)^2-20x+21$

$=\,\,\,$ $(2x)^2-2 \times 10x+21$

$=\,\,\,$ $(2x)^2-2 \times 5 \times 2x+21$

$=\,\,\,$ $(2x)^2-2 \times 2x \times 5+21$

Now, add the square of $5$ to the above polynomial and subtract the same quantity from it.

$=\,\,\,$ $(2x)^2-2 \times 2x \times 5+5^2-5^2+21$

$=\,\,\,$ $(2x)^2+5^2-2 \times 2x \times 5-5^2+21$

$=\,\,\,$ $(2x)^2+5^2-2 \times 2x \times 5-25+21$

$=\,\,\,$ $\big((2x)^2+5^2-2 \times 2x \times 5\big)-4$

$=\,\,\,$ $(2x-5)^2-4$

$\therefore\,\,\,$ $4x^2-20x+21$ $\,=\,$ $(2x-5)^2-4$

Therefore, the quadratic expression $4x^2-20x+21$ is transformed as $(2x-5)^2-4$ successfully.

Usage

Completing the square method is used to find the roots (or zeros) of the quadratic equations. Firstly, let’s learn how to derive the quadratic formula for the quadratic equation in standard form by completing the square method.

Problems

List of the math problems with solutions to learn how to use completing the square method in mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.