Quadratic formula

Formula

$x \,=\, \dfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$

A formula that expresses the solution of a quadratic equation is called the quadratic formula.

Introduction

The quadratic equations often come into our way and we have to find the roots of them. In mathematics, we have some fundamental methods to solve the zeros of any quadratic equation but they take some time to solve. Hence, the idea of deriving a formula for solving any quadratic equation comes into action.

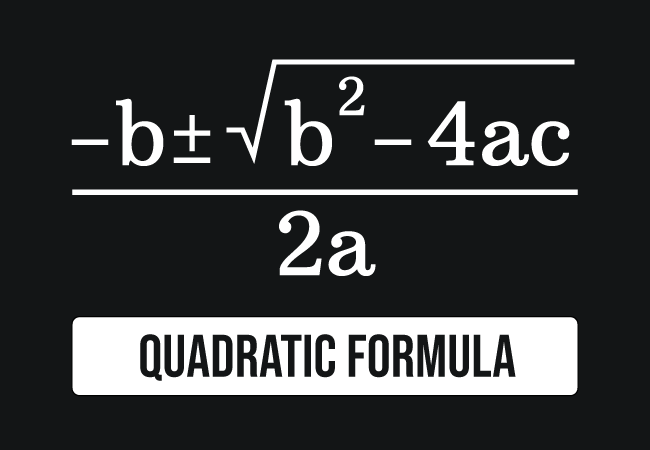
A quadratic equation is written as $ax^2+bx+c = 0$ mathematically in general form in mathematics. The following is the solution of this standard form equation.

$x$ $\,=\,$ $\dfrac{-b \pm \sqrt{b^2 -4ac}}{2a}$

It is used to find the roots of any quadratic equation. So, it is called the quadratic formula.

The quadratic equation is a second degree polynomial. So, it has two roots. If the two zeros (or roots) are denoted by alpha and beta, then the quadratic formula is used to find the zeros in the following way.

$(1).\,\,\,$ $\alpha$ $\,=\,$ $\dfrac{-b+\sqrt{b^2-4ac}}{2a}$

$(2).\,\,\,$ $\beta$ $\,=\,$ $\dfrac{-b-\sqrt{b^2-4ac}}{2a}$

Example

Solve $2x^2+5x-12 = 0$

In this case, $a = 2$, $b = 5$ and $c = -12$. Substitute all of them in the quadratic formula.

$x$ $\,=\,$ $\dfrac{-5 \pm \sqrt{5^2 -4 \times 2 \times (-12)}}{2 \times 2}$

$\implies$ $x$ $\,=\,$ $\dfrac{-5 \pm \sqrt{25-8 \times (-12)}}{4}$

$\implies$ $x$ $\,=\,$ $\dfrac{-5 \pm \sqrt{25+96}}{4}$

$\implies$ $x$ $\,=\,$ $\dfrac{-5 \pm \sqrt{121}}{4}$

$\implies$ $x$ $\,=\,$ $\dfrac{-5 \pm 11}{4}$

If the zeros of this quadratic equation are represented by alpha and beta, then the solution of this example quadratic equation is evaluated as follows.

$\implies$ $\alpha$ $\,=\,$ $\dfrac{-5+11}{4}$ and $\beta$ $\,=\,$ $\dfrac{-5-11}{4}$

$\implies$ $\alpha$ $\,=\,$ $\dfrac{6}{4}$ and $\beta$ $\,=\,$ $\dfrac{-16}{4}$

$\implies$ $\alpha$ $\,=\,$ $\dfrac{\cancel{6}}{\cancel{4}}$ and $\beta$ $\,=\,$ $\dfrac{-\cancel{16}}{\cancel{4}}$

$\,\,\,\therefore\,\,\,\,\,\,$ $\alpha$ $\,=\,$ $\dfrac{3}{2}$ and $\beta$ $\,=\,$ $-4$

Proof

Learn how to prove the quadratic formula in mathematics fundamentally by completing the square.

Problems

List of questions on quadratic equations with solutions to learn how to solve a quadratic equation by the quadratic formula.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.