ASA Criterion for Congruence of Triangles

The triangles are congruent when two angles and the included side of one triangle are equal to the corresponding two angles and the included angle of the other triangle. It is called the Angle-Side-Angle (ASA) criterion for the congruence of triangles.

Introduction

In each triangle, there are three sides and three angles. The congruence of any two triangles can be determined by comparing the corresponding two angles and corresponding one included side of them.

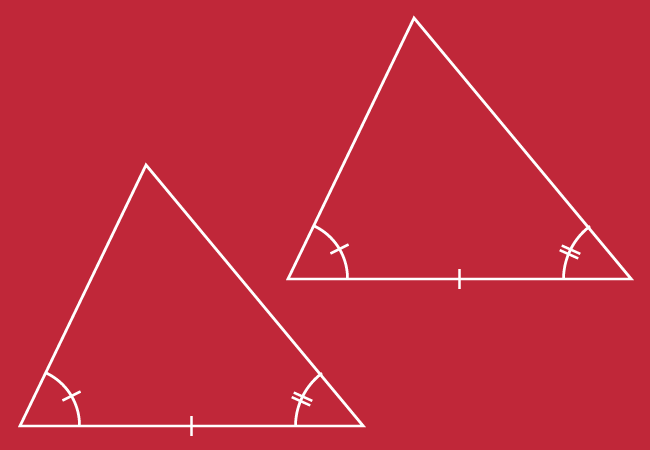
If two angles and length of the included side of one triangle are equal to the corresponding two angles and corresponding length of included side of other triangle, then the two triangles are congruent geometrically. Therefore, the triangles are called the congruent triangles.

The comparison of corresponding two angles and corresponding the included side of both triangles is a criteria for checking the congruence of any two triangles. Therefore, it is called angle-side-angle criterion and it is simply called as ASA criterion for congruence of triangles.

The ASA (Angle-Side-Angle) criterion can be learnt from an understandable example in detail.

Example

$\Delta CDE$ and $\Delta JKL$ are two triangles but their angles and lengths of sides are unknown. However, the two angles angle and length of one included side of every triangle can be measured by a protractor and a ruler respectively.

It is measured that

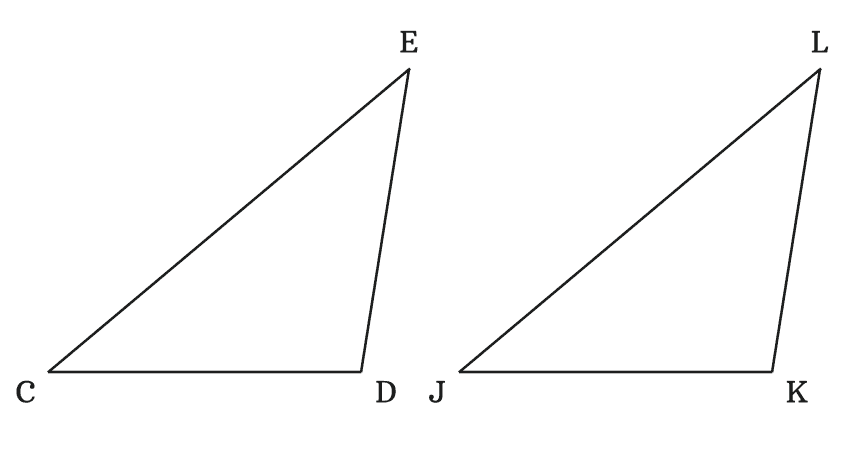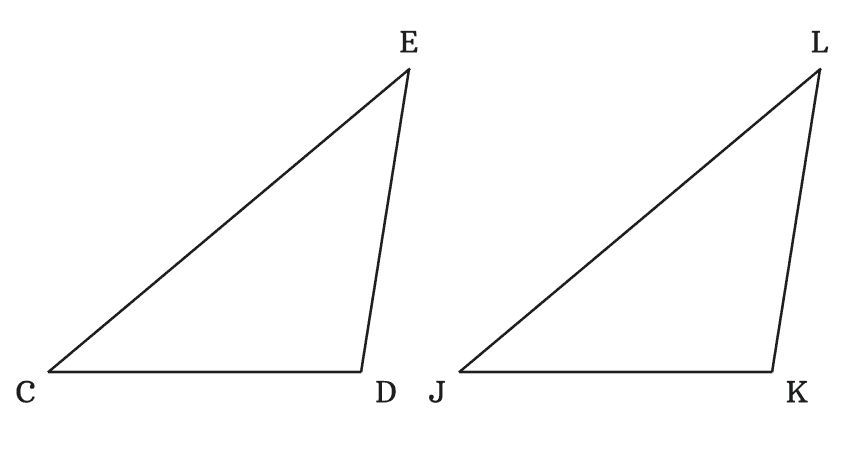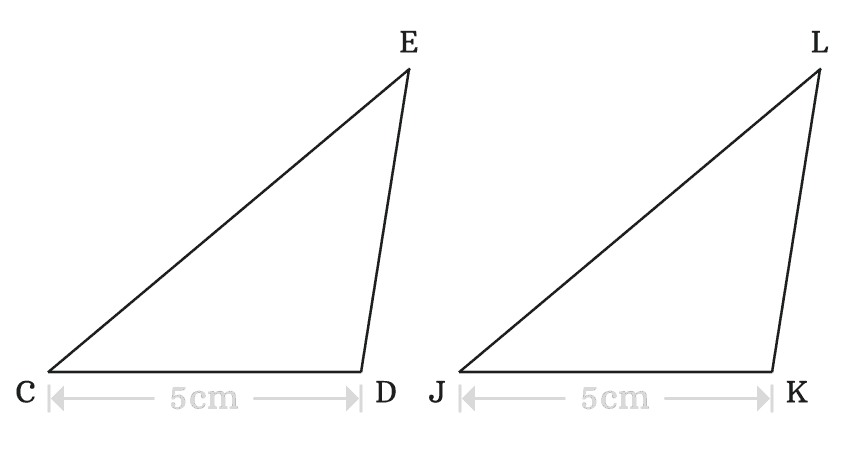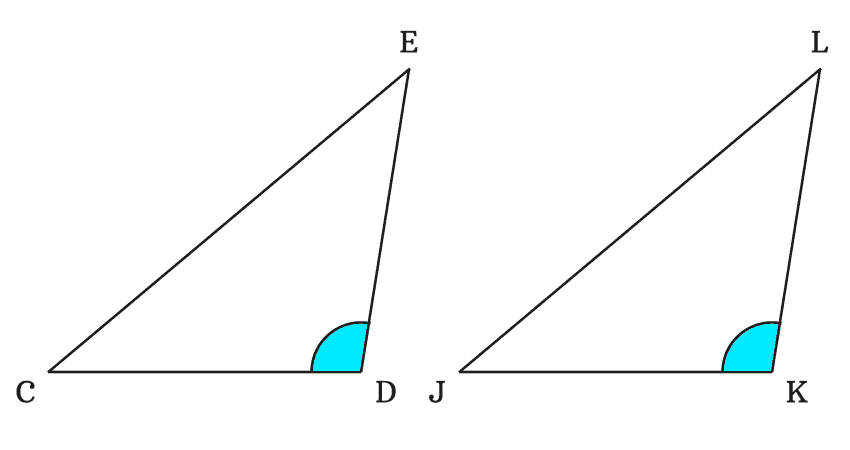
In $\Delta CDE$, $\angle ECD \,=\, 40^°$, $CD \,=\, 5\,cm$ and $\angle CDE \,=\, 99^°$

In $\Delta JKL$, $\angle LJK \,=\, 40^°$, $JK \,=\, 5\,cm$ and $\angle JKL \,=\, 99^°$

Now, compare the corresponding angles and length of included side of both triangles.

$(1).\,\,\,$ $\angle ECD \,=\, \angle LJK \,=\, 40^°$

$(2).\,\,\,$ $CD \,=\, JK \,=\, 5\,cm$

$(3).\,\,\,$ $\angle CDE \,=\, \angle JKL \,=\, 99^°$

We can observe that the corresponding angles and the length of included side of both triangle are equal. Therefore, the two triangles are called the congruent triangle.

$\therefore \,\,\,\,\,\,$ $\Delta CDE \,\cong\, \Delta JKL$

In this example, the two corresponding angle and the length of one included side are considered as a criteria for determining congruence of the triangles. Hence, the criteria is called ASA (Angle-Side-Angle) criterion in geometry.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.