Unlike fractions

The two or more fractions that contain different denominators are called the unlike fractions.

Introduction

In some cases, if we observe two or more fractions, they may have different denominators and it seems they are dissimilar. So, the fractions are called the unlike fractions.

The unlike fractions are possibly formed if every quantity is divided as different number of parts and it breaks the similarity between them. Hence, the fractions become dissimilar.

Example

The concept of unlike fractions can be understood from an example with geometrical explanation.

1. Take a circle and split it into four equal parts. If we select a part from first circle, then the fraction is equal to $\large \frac{1}{4}$
2. Take another circle and split it into five equal parts. If we select three parts from second circle, then the fraction is equal to $\large \frac{3}{5}$
3. Take three circles and divide each circle into three equal parts. If we select eight parts from the remaining three circles, then the fraction is equal to $\large \frac{8}{3}$

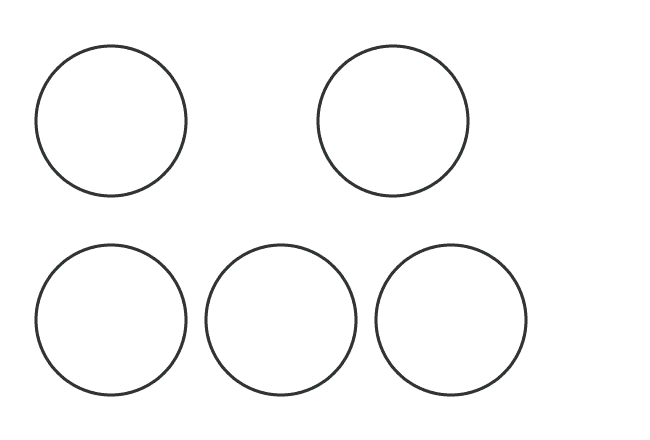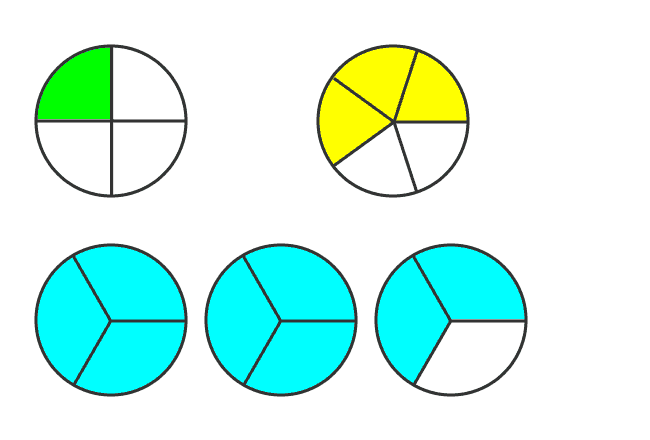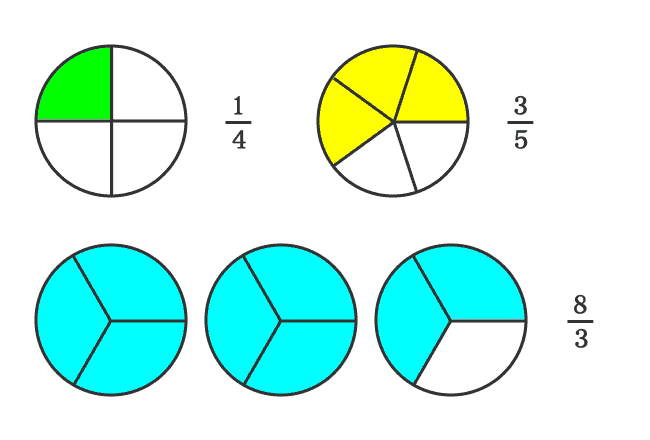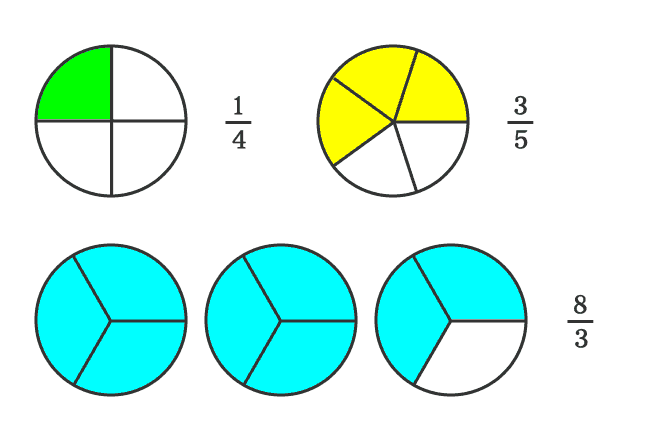
In this way, two proper fractions $\dfrac{1}{4}$ and $\dfrac{3}{5}$, and an improper fraction $\dfrac{8}{3}$ are formed. In this case, the denominators (consequent) are different. Therefore, the fractions are called as unlike fractions.

Therefore, the unlike fractions can be either proper fractions or improper fractions or both.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.