Third Quadrant

The left-bottom side region in the two dimensional space is called the third quadrant.

Introduction

Two number lines are perpendicularly bisected at their middle point in bi-dimensional Cartesian coordinate system for splitting the coordinate plane into four equal regions.

The left-bottom side region is called the third quadrant. In this case, the region in the angle $X’OY’$ is the third quadrant and represented by a Roman numeral $III$.

In $\angle X’OY’$, the $x$-axis and $y$-axis both represent negative values. Therefore, the abscissa and ordinate of every point in this region should be negative.

If $x$-coordinate and $y$-coordinate of each point are denoted by $x$ and $y$ respectively, then the values of both coordinates are written in mathematical form as $x < 0$ and $y < 0$.

Usage

The third quadrant is used in the bi dimensional space to identity the location of a point whose abscissa and ordinate are negative. So, let’s study how to use the third quadrant in coordinate geometry.

Example

Identify the location of the point $C(-6, -4)$.

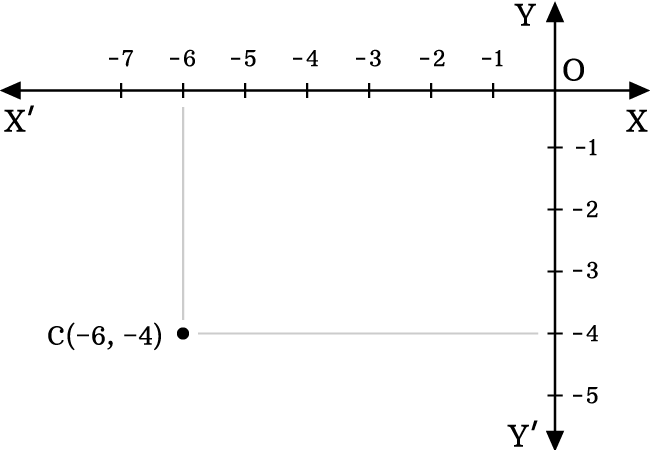
Here, the $x$ coordinate (or abscissa) is $-6$ and $y$ coordinate (or ordinate) is $-4$.

Identity $-6$ on negative $x$-axis. Draw a line from $-6$ but it should be parallel to negative $y$ axis and perpendicular to negative $x$ axis.
Identify $-4$ on negative $y$ axis. Draw a line from $-4$ but it should be perpendicular to negative $y$ axis and parallel to negative $x$ axis.
The two straight lines are perpendicularly intersected at a point in the plane and it is the point $C(-6, -4)$.

In this way, the third quadrant of two dimensional Cartesian coordinate system is used for identifying the location of any point whose both abscissa and ordinate are negative.