A straight line that touches a circle at one point is called a tangent line to a circle.
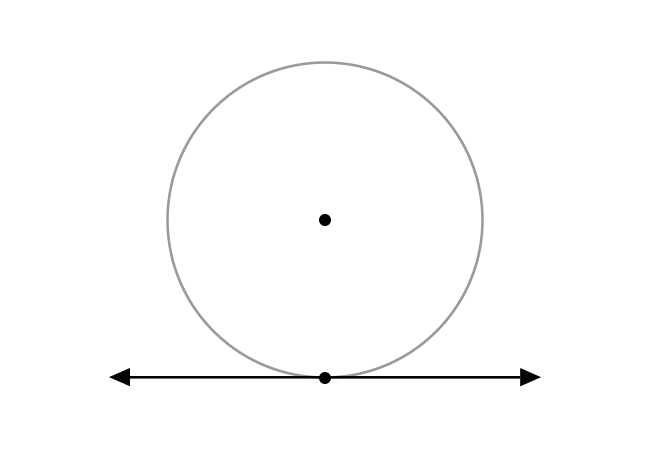
In geometric mathematics, the straight lines are often passed through some points of the circles for some reasons but some of them do not enter into the interior of the circles. It is possible when the straight lines touch the circles exactly at only one point. In this case, the straight lines are called the tangent lines to circles.
The tangent line of a circle is perpendicular to a line that represents the radius of a circle.
Now, let’s learn the concept of tangent of a circle from an understandable example here.
Consider a circle in a plane and assume that $S$ is a point in the plane but it is outside of the circle. Now, draw a straight line from point $S$ and assume that it touches the circle at a point $T$. The straight line $\overleftrightarrow{TS}$ is called a tangent line to the circle.
Now, connect the point $T$ with the center (or centre) of circle by a line. The line segment $\overline{CT}$ represents the radius of this circle. Geometrically, the radius line $\overline{CT}$ and the tangent line $\overleftrightarrow{TS}$ are perpendicular lines at point $T$.
It clears that a tangent to a circle at a point is a perpendicular to the radius line at that point.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2023 Math Doubts, All Rights Reserved