Subsets

A set whose all elements are elements of another set is called a subset.

Introduction

The collection of well defined objects form sets in mathematics. In some cases, the members in a set are also elements of another set. Hence, a set of which all the elements are contained in another set is called a subset.

The concept of a subset can be understood here from a basic example.

There are seven students in a classroom in which four students are boys and three students are girls.

1. The collection of seven students is a set.
2. The collection of four boys is another set.
3. The collection of three girls is also another set.

Here, we have three sets. They are a class set, a boys set and a girls set.

1. The four boys are basically a set but they are also members of a class. Hence, the boys set is called a subset of the class set.
2. Similarly, the three girls are also a set and they are also members of the same class. Hence, the girls set is also called a subset of the class set.

Representation

A symbol $\subseteq$ was introduced in set theory to express a phrase “is a subset of” symbolically.

$Boys \, set \subseteq Class \, set$

It expresses that the boys set is a subset of the class set.

$Girls \, set \subseteq Class \, set$

It expresses that the girls set is a subset of the class set.

Example

Let’s learn the concept of subset from a numerical example.

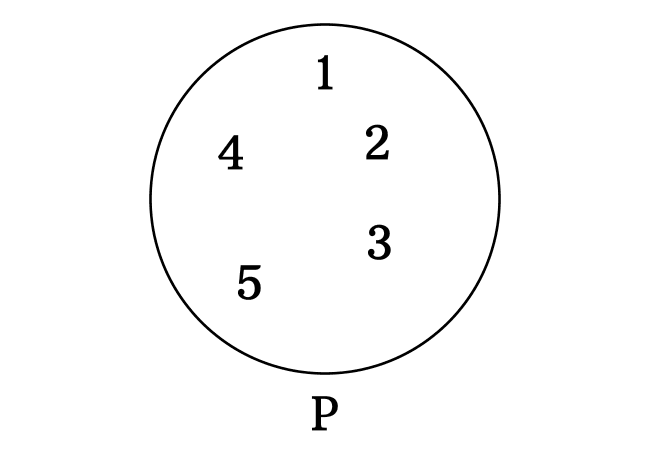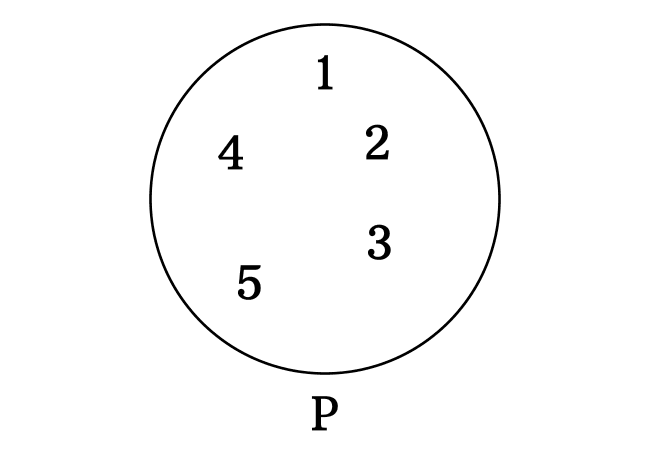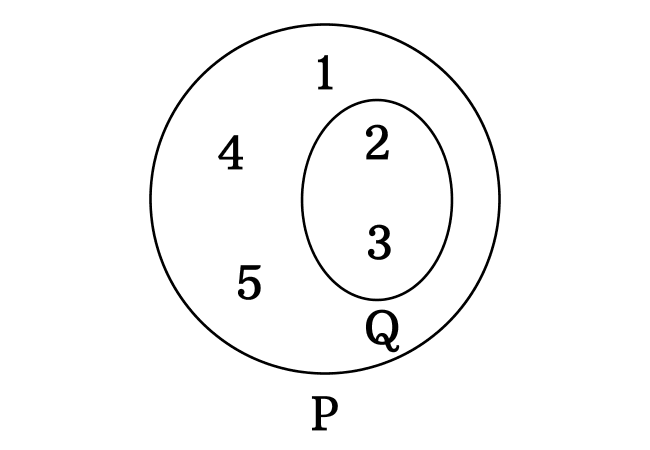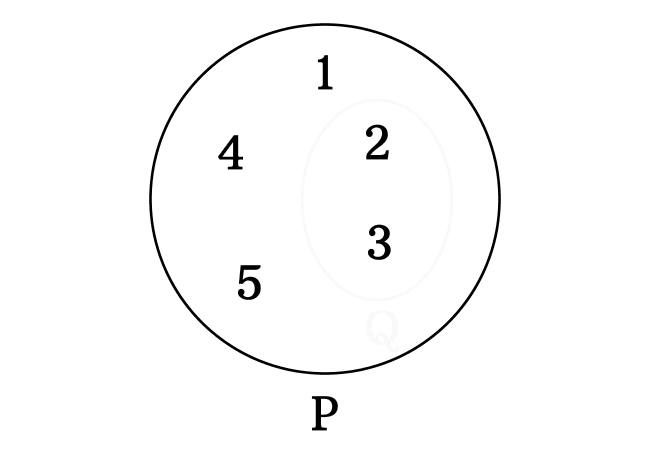
$P$ $\,=\,$ $\Big\{$ $1, 2, 3, 4, 5$ $\Big\}$

$Q$ $\,=\,$ $\Big\{$ $2, 3$ $\Big\}$

$P$ and $Q$ are two sets. The set $P$ contains five elements and the set $Q$ contains two members.

The numbers $2$ and $3$ are elements of set $Q$ but they also belong to set $P$. Hence, the set $Q$ is called a subset of set $P$ and it is mathematically expressed in the following form in the set theory.

$Q \subseteq P$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.