Proof of standard equation of a circle

The equation of a circle in standard form is popularly written in the following two forms in mathematics.

$(1).\,\,\,$ $(x-a)^2+(y-b)^2$ $\,=\,$ $r^2$

$(2).\,\,\,$ $(x-h)^2+(y-k)^2$ $\,=\,$ $r^2$

Now, let’s learn how to prove the standard form equation of a circle mathematically as per the geometric system when the circle does not touch both axes in two dimensional cartesian coordinate system.

Construction of a Triangle inside a Circle

A right triangle or right angled triangle should be constructed inside a circle when the circle does not touch both $x$ axis and $y$ axis in a quadrant of two-dimensional cartesian coordinate system. It helps us to express the equation of a circle in mathematical form.

The following five steps are the steps for the geometrical construction of a right angled triangle inside a circle when the circle does not touch both axes.

1. Consider the first quadrant of bi-dimensional cartesian coordinate system and draw a circle in such a way that it does not touch any axis.
2. Let’s denote the center (or centre) of a circle by $C$. Assume that, the centre (or center) is $a$ and $b$ units away from the origin in horizontal and vertical directions respectively. So, the center (or centre) is expressed as $C(a, b)$ in coordinate form mathematically.
3. $P$ is a point on the circumference of circle. Assume that the point $P$ is $x$ and $y$ units away from the origin in horizontal and vertical directions. Therefore, the point $P$ is written as $P(x, y)$ in coordinate form.
4. Now, draw a straight line from center $C$ to point $P$ for connecting them and the line segment $\overline{CP}$ represents the radius in the circle. Assume that the length of the radius is $r$ units.
5. Finally, draw a straight line horizontally from centre (or center) until it touches a point on the circumference of circle. Similarly, draw a straight line from $P$ in downward direction until it intersects the horizontal line at point $Q$. Thus, right angled triangle is formed geometrically and it is written as $\Delta QCP$ in mathematics.

Find the lengths of all sides of Triangle

In $\Delta QCP$, $\overline{PQ}$ is opposite side, $\overline{CQ}$ is adjacent side and $\overline{CP}$ is hypotenuse, and the lengths of them are written as $PQ, CQ$ and $CP$ respectively.

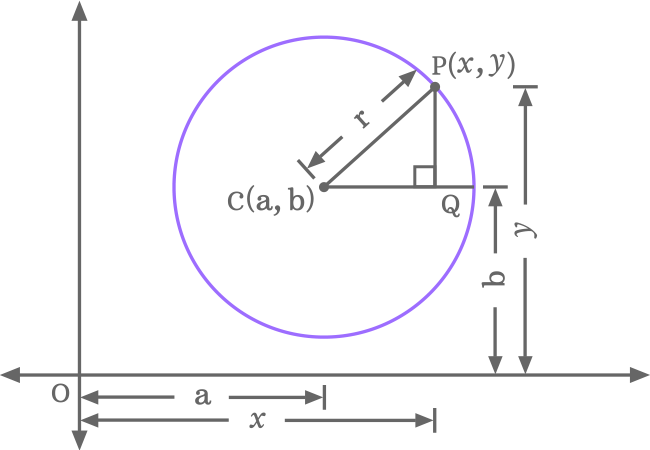
Now, let’s calculate the length of every side in the right triangle.

1. $CQ$ $\,=\,$ $OQ\,–\,OC$ $\,=\,$ $x \,–\,a$
2. $PQ$ $\,=\,$ $OP\,–\,OQ$ $\,=\,$ $y\,-\,b$
3. $CP \,=\, r$.

Write the relation between the sides

The length of each side of right triangle $QCP$ is evaluated and it is time express the mathematical relation between the lengths of the sides. It can be done as per the Pythagorean Theorem.

${CP}^2$ $\,=\,$ ${CQ}^2+{PQ}^2$

Here, $CP, CQ$ and $PQ$ are the lengths of the hypotenuse, adjacent side and opposite side respectively. Now, substitute the lengths of the sides in the above equation.

$\implies$ $r^2$ $\,=\,$ $(x-a)^2+(y-b)^2$

$\,\,\,\therefore\,\,\,\,\,\,$ $(x-a)^2+(y-b)^2$ $\,=\,$ $r^2$

It is called the equation of a circle in standard form when the $C(a, b)$ is center (or centre) in coordinate form and the radius of the circle is $r$ units.

Other form

The equation of a circle in standard form is also popularly written in the following form when the coordinates of center (or centre) are denoted by $h$ and $k$. It the centre (or center) in coordinate form is written as $C(h, k)$ and the radius is denoted by $r$.

$(x-h)^2+(y-k)^2$ $\,=\,$ $r^2$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.