Solve $\log_{7}{\log_{5}{\sqrt{x+5}+\sqrt{x}}} \,=\, 0$

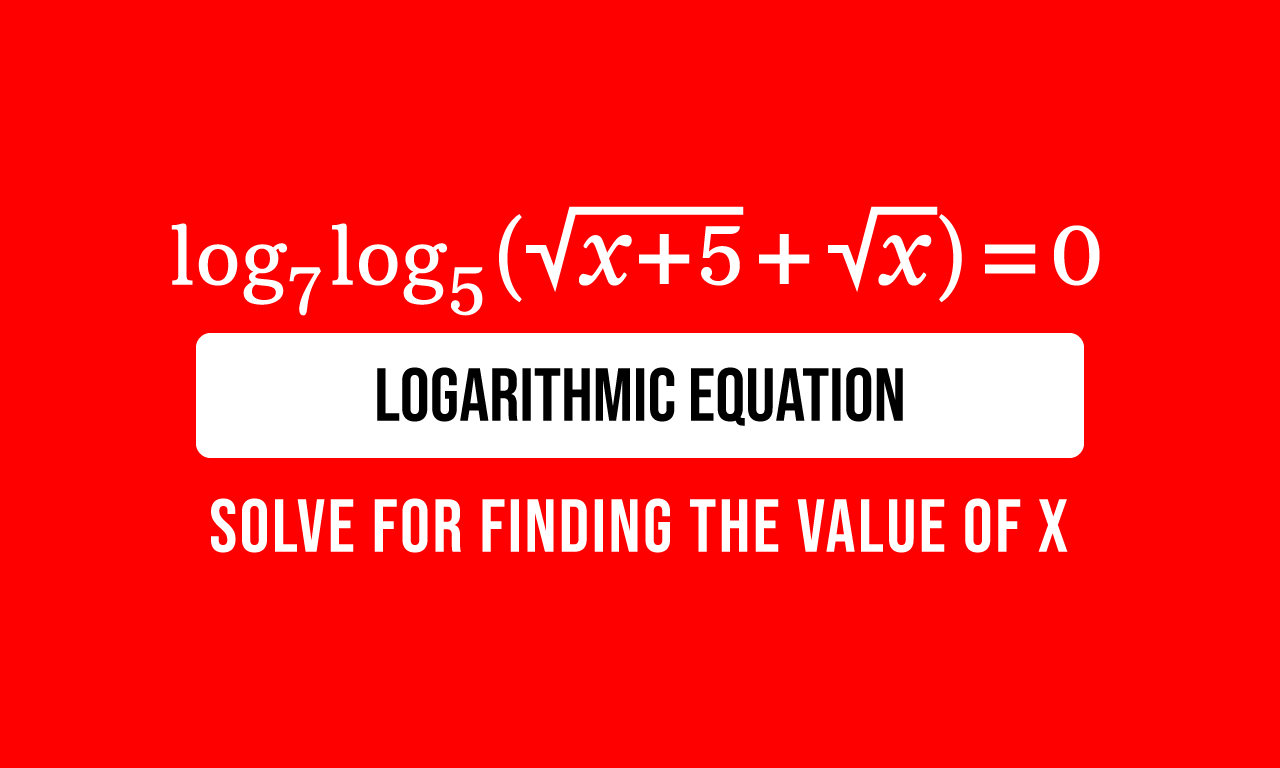
The logarithm of the logarithm of square root of $x$ plus $5$ plus square root of $x$ to the base $5$, to the base $7$ equals to zero is the given logarithmic equation in this problem.

$\log_{7}{\Big(\log_{5}{\big(\sqrt{x+5}+\sqrt{x}\big)}\Big)}$ $\,=\,$ $0$

The value of the variable $x$ is unknown in this equation and it should be solved in this logarithmic equation problem. So, let’s learn how to find the value of the variable $x$ by solving this logarithmic equation.

Remove the Logarithms from the equation

The logarithmic form in the equation initially creates the hurdles for solving the equation. Therefore, eliminating the logarithmic form is a recommendable trick for solving the given logarithmic equation. It can be done by using the mathematical relationship between logarithms and exponents.

$\implies$ $\log_{5}{\big(\sqrt{x+5}+\sqrt{x}\big)}$ $\,=\,$ $7^{0}$

According to the zero power rule, seven raised to the power of zero is equal to one.

$\implies$ $\log_{5}{\big(\sqrt{x+5}+\sqrt{x}\big)}$ $\,=\,$ $1$

Eliminate the Logarithm completely from equation

The logarithm is still involved in the equation with base five. So, use the relation between the logarithms and exponents one more time for completely removing the logarithm from the equation.

$\implies$ $\sqrt{x+5}$ $+$ $\sqrt{x}$ $\,=\,$ $5^1$

Solve the irrational equation by simplification

The given logarithmic equation is successfully converted into an irrational equation by releasing the equation from the logarithms.

$\implies$ $\sqrt{x+5}$ $+$ $\sqrt{x}$ $\,=\,$ $5$

Look at the algebraic expression on the left hand side of the equation. It is completely in irrational form and this irrational form creates problem for finding the value of the variable $x$. So, it is recommended to eliminate the irrational form from the equation.

Shift the square root of $x$ from the left hand side to right hand side of the equation by transposition for initiating the process of eliminating the irrational form the equation completely.

$\implies$ $\sqrt{x+5}$ $\,=\,$ $5-\sqrt{x}$

Take the square for the both expressions in order to try to eliminate the square root from the equation.

$\implies$ $(\sqrt{x+5})^2$ $\,=\,$ $(5-\sqrt{x})^2$

$\implies$ $x+5$ $\,=\,$ $(5-\sqrt{x})^2$

On the right hand side of the equation, expand the square of difference of the terms by using the square of difference rule.

$\implies$ $x+5$ $\,=\,$ $5^2$ $+$ $(\sqrt{x})^2$ $-$ $2 \times 5 \times \sqrt{x}$

Now, simplify the mathematical equation in algebraic form by transposing.

$\implies$ $x+5$ $\,=\,$ $25$ $+$ $x$ $-$ $10\sqrt{x}$

$\implies$ $10\sqrt{x}$ $\,=\,$ $25$ $+$ $x$ $-$ $x$ $-$ $5$

$\implies$ $10\sqrt{x}$ $\,=\,$ $25$ $-$ $5$ $+$ $x$ $-$ $x$

$\implies$ $10\sqrt{x}$ $\,=\,$ $20$ $+$ $\cancel{x}$ $-$ $\cancel{x}$

$\implies$ $10\sqrt{x}$ $\,=\,$ $20$

$\implies$ $10 \times \sqrt{x}$ $\,=\,$ $20$

$\implies$ $\sqrt{x}$ $\,=\,$ $\dfrac{20}{10}$

$\implies$ $\sqrt{x}$ $\,=\,$ $\dfrac{\cancel{20}}{\cancel{10}}$

$\implies$ $\sqrt{x}$ $\,=\,$ $2$

The equation is successfully simplified by it is still in irrational form. So, use the same technique to eliminate the irrational form the equation by taking square on both sides.

$\implies$ $(\sqrt{x})^2$ $\,=\,$ $2^2$

$\,\,\,\therefore\,\,\,\,\,\,$ $x$ $\,=\,$ $4$

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.