Proof of Sine double angle identity

The sine of double angle identity is a trigonometric identity and used as a formula. It is usually written in the following three popular forms for expanding sine double angle functions in terms of sine and cosine of angles.

$(1).\,\,\,$ $\sin{(2\theta)}$ $\,=\,$ $2\sin{\theta}\cos{\theta}$

$(2).\,\,\,$ $\sin{(2A)}$ $\,=\,$ $2\sin{A}\cos{A}$

$(3).\,\,\,$ $\sin{(2x)}$ $\,=\,$ $2\sin{x}\cos{x}$

The sine double angle rule can be proved in mathematical form geometrically from a right triangle (or right angled triangle). It is your turn to learn the geometric proof of sin double angle formula.

Construction

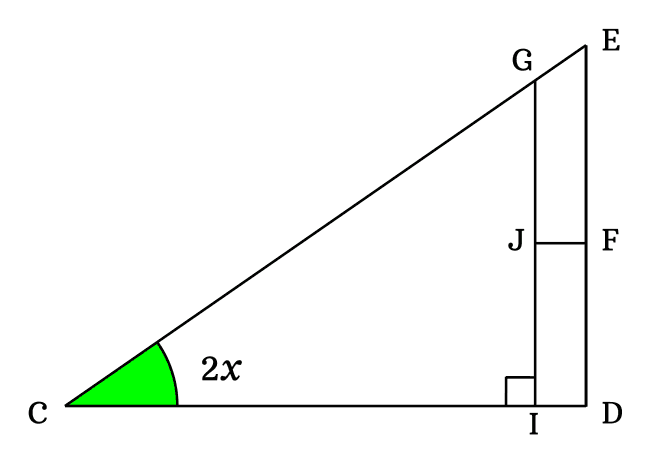
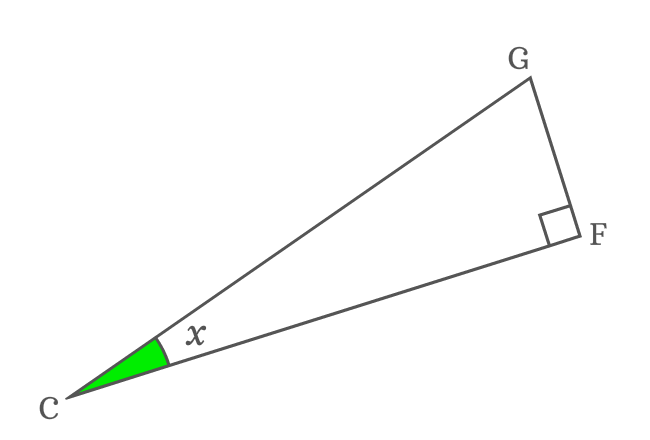
Let’s consider a right angled triangle. Here, it is $\Delta ECD$. We have to do some geometric settings inside this right triangle by following below steps.

1. Bisect the angle $DCE$ by drawing a straight line from point $C$ to side $\overline{DE}$ and it intersects the side $\overline{DE}$ at point $F$. Each angle is represented by a variable $x$.
2. Draw a line to side $\overline{CE}$ from point $F$ but it should be perpendicular to side $\overline{CF}$. Assume that it intersects the side $\overline{CE}$ at point $G$.
3. Draw a perpendicular line to side $\overline{CD}$ from point $\small G$. It intersects the side $\overline{CF}$ at point $H$ and perpendicularly intersects side $\overline{CD}$ at point $I$.
4. Draw a perpendicular line to side $\small \overline{GI}$ from point $\small F$ and it intersects the side $\small \overline{GI}$ at point $\small J$.

Now, we can start deriving the expansion of the sine of double angle trigonometric identity in mathematical form.

Procedure

When $x$ is used to represent an angle of a right triangle, the sine, cosine and sine of double angle functions are written as $\sin{x}$, $\cos{x}$ and $\sin{2x}$ respectively.

Express the Sine of double angle in Ratio form

The side $\overline{CF}$ bisects the $\angle DCE$ as two equal angles $\angle DCF$ and $\angle FCE$. Here, the $\angle DCF$ and $\angle FCE$ are equal and each angle is denoted by $x$.

$\angle DCE$ $\,=\,$ $\angle DCF + \angle FCE$

$\implies$ $\angle DCE \,=\, x+x$

$\,\,\,\therefore\,\,\,\,\,\,$ $\angle DCE \,=\, 2x$

It is cleared that the angle $DCE$ is equal to $2x$. Hence, the sine of angle $2x$ is written as $\sin{(2x)}$ in trigonometric mathematics.

According to the $\Delta ICG$, the sine of double angle can be written in ratio form of the lengths of the sides.

$\sin{2x} \,=\, \dfrac{GI}{CG}$

The side $\overline{JF}$ splits the side $\overline{GI}$ as two sides $\overline{GJ}$ and $\overline{JI}$. So, the length of side $\overline{GI}$ can be written as the sum of them mathematically.

$GI = GJ + JI$

Now, replace the length of side $\overline{GI}$ by its equivalent value in the expansion of $\sin{(2x)}$ function.

$\implies$ $\sin{2x}$ $\,=\,$ $\dfrac{GJ+JI}{CG}$

$\implies$ $\sin{2x}$ $\,=\,$ $\dfrac{GJ}{CG}+\dfrac{JI}{CG}$

The sides $\overline{GI}$ and $\overline{DE}$ are parallel lines. So, the length of the side $\overline{JI}$ is exactly equal to the length of the side $\overline{DF}$. Therefore, $JI = DF$.

$\implies$ $\sin{2x}$ $\,=\,$ $\dfrac{GJ}{CG}+\dfrac{DF}{CG}$

Express trigonometric ratios in functions

The $\sin{(2x)}$ is expanded in terms of the ratios between the sides. Now, let’s try to express each ratio in the form a trigonometric function.

The side $\overline{EF}$ is opposite side of the $\Delta ECF$ and its angle is $x$. Try to write the length of side $\overline{EF}$ in terms of a trigonometric function.

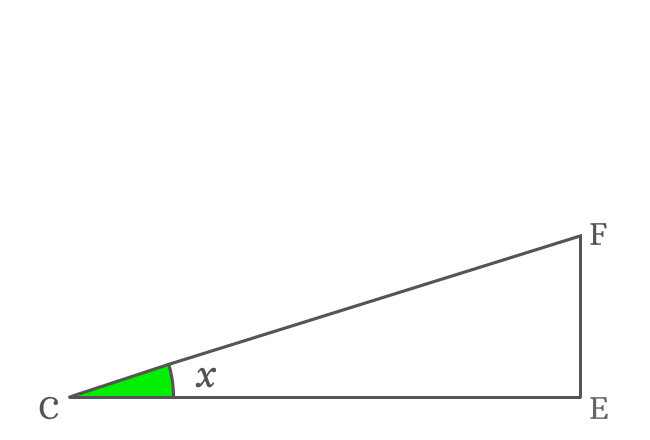
$\sin{x} = \dfrac{EF}{CF}$

$\implies EF = {CF}\sin{x}$

Now, substitute the length of perpendicular $\overline{EF}$ by its equivalent value in the expansion of $\sin{2x}$.

$\implies$ $\sin{2x} \,=\, \dfrac{GJ}{CG}+\dfrac{{CF}\sin{x}}{CG}$

$\implies$ $\sin{2x} \,=\, \dfrac{GJ}{CG}+\dfrac{CF}{CG} \times \sin{x}$

The sides $\overline{CF}$ and $\overline{CG}$ are sides of the right triangle $GCF$ and the angle of this triangle is also $x$. According to trigonometry, the ratio of them can be represented by $\cos{x}$.

$\cos{x} = \dfrac{CF}{CG}$

Now, replace the ratio of lengths of sides $\overline{CF}$ to $\overline{CG}$ by its equivalent trigonometric function in the expansion of sin of double angle function.

$\implies$ $\sin{2x} \,=\, \dfrac{GJ}{CG}+\cos{x} \times \sin{x}$

$\implies$ $\sin{2x} \,=\, \dfrac{GJ}{CG}+\cos{x}\sin{x}$

$\implies$ $\sin{2x} \,=\, \dfrac{GJ}{CG}+\sin{x}\cos{x}$

Geometric Analysis for unknown angle

The side $\overline{GJ}$ is one of the sides of the $\Delta JGF$ but its angle is unknown. So, it is not possible to express the length of the side $\overline{GJ}$ in terms of a trigonometric function. Hence, let’s find the angle of this triangle geometrically.

The sides $\overline{CE}$ and $\overline{JF}$ are parallel lines and $\overline{CF}$ is their transversal. $\angle ECF$ and $\angle JFC$ are interior alternate angles and they are equal geometrically.

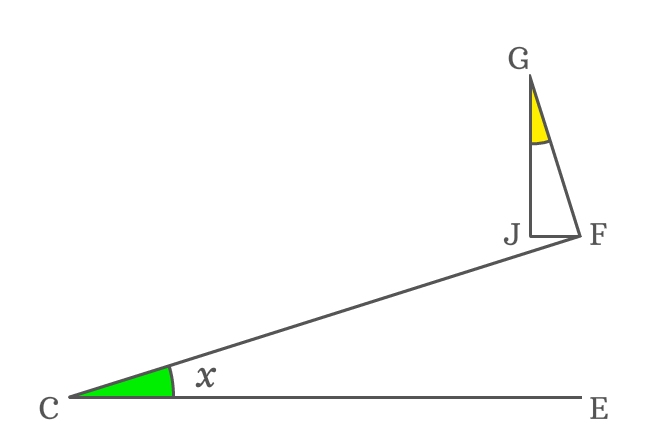
$\angle JFC = \angle ECF = x$

The side $\overline{FG}$ is a perpendicular line to side $\overline{CF}$. So, the $\angle CFG = 90^°$. but the side $\overline{JF}$ splits the $\angle CFG$ as $\angle JFC$ and $\angle JFG$.

$\angle JFC + \angle JFG = 90^°$

It is proved about that $\angle JFC = x$.

$\implies x + \angle JFG = 90^°$

$\implies \angle JFG = 90^°-x$

$\Delta JGF$ is a right triangle in which $\angle GJF = 90^°$ and $\angle JFG = 90^°-x$. The $\angle JGF$ can be calculated by the sum of angles rule of a triangle.

$\angle JGF + \angle GJF + \angle JFG$ $=$ $180^°$

$\implies \angle JGF + 90^° + 90^°-x$ $=$ $180^°$

$\implies \angle JGF + 180^°-x$ $=$ $180^°$

$\implies \angle JGF $ $=$ $180^°-180^°+x$

$\,\,\, \therefore \,\,\,\,\,\, \angle JGF = x$

It is proved that the $\angle JGF$ is also equal to $x$ because it is a similar triangle.

Write trigonometric ratio in functions

It is already derived that

$\sin{2x} \,=\, \dfrac{GJ}{CG}+\sin{x}\cos{x}$

Now, let’s try to write the ratio between sides $\overline{GJ}$ and $\overline{CG}$ in terms of trigonometric functions to get the expansion of sin double angle identity.

$\overline{GJ}$ is adjacent side of $\Delta JGF$ and its angle is derived as $x$.

$\cos{x} = \dfrac{GJ}{GF}$

$\implies GJ = {GF}\cos{x}$

Substitute the length of $\overline{GJ}$ by its equivalent value in the expansion of $\sin{(2x)}$ function.

$\sin{2x}$ $\,=\,$ $\dfrac{{GF}\cos{x}}{CG}+\sin{x}\cos{x}$

$\implies \sin{2x}$ $\,=\,$ $\dfrac{GF}{CG} \times \cos{x}+\sin{x}\cos{x}$

The sides $\overline{GF}$ and $\overline{CG}$ are sides of $\Delta GFC$. So, consider right triangle $GFC$ once more time.

$\sin{x} = \dfrac{GF}{CG}$

Therefore, replace the ratio of lengths of sides $\overline{GF}$ to $\overline{CG}$ by trigonometric function $\sin{x}$ in the $\sin{2x}$ expansion.

$\implies \sin{2x}$ $\,=\,$ $\sin{x} \times \cos{x}+\sin{x}\cos{x}$

$\implies \sin{2x}$ $\,=\,$ $\sin{x}\cos{x}+\sin{x}\cos{x}$

$\,\,\, \therefore \,\,\,\,\,\, \sin{2x}$ $\,=\,$ $2\sin{x}\cos{x}$

Therefore, it is proved geometrically that the sin of double angle function can be expanded as two times the product of sin of angle and cos of angle.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.