The sum of angles trigonometric formula for sin function is usually expressed as $\sin{(A+B)}$ or $\sin{(x+y)}$ in trigonometric mathematics generally. You learned how to expand sin of sum of two angles by this angle sum identity. It is time to learn how to prove the expansion of sine of compound angle rule in trigonometry.
$(1).\,\,$ $\sin{(a+b)}$ $\,=\,$ $\sin{a}\cos{b}$ $+$ $\cos{a}\sin{b}$
$(2).\,\,$ $\sin{(x+y)}$ $\,=\,$ $\sin{x}\cos{y}$ $+$ $\cos{x}\sin{y}$
$(3).\,\,$ $\sin{(\alpha+\beta)}$ $\,=\,$ $\sin{\alpha}\cos{\beta}$ $+$ $\cos{\alpha}\sin{\beta}$
$\Delta DCE$ is a right triangle and its angle is divided as two angles to derive a trigonometric identity for the sine of sum of two angles.
$(1). \,\,\,$ Draw a straight line from point $C$ towards side $\overline{DE}$ to divide the $\angle DCE$ as two angles $x$ and $y$. The line intersects the side $\overline{DE}$ at point $F$.
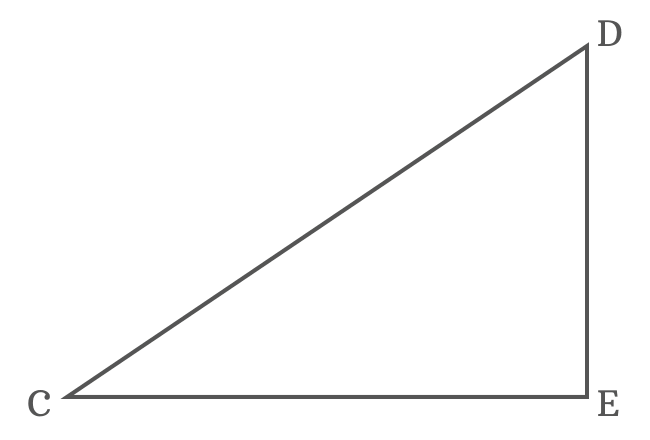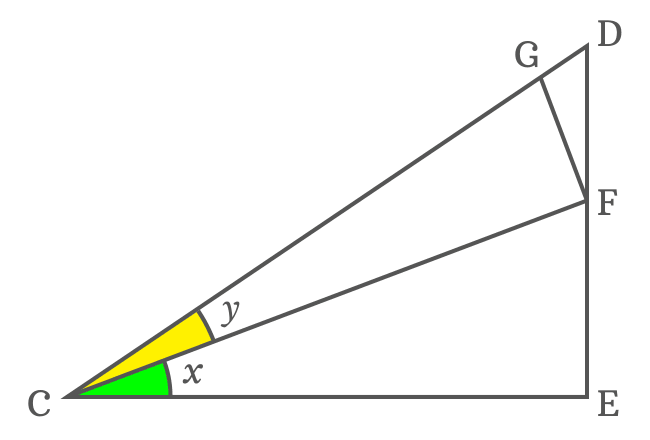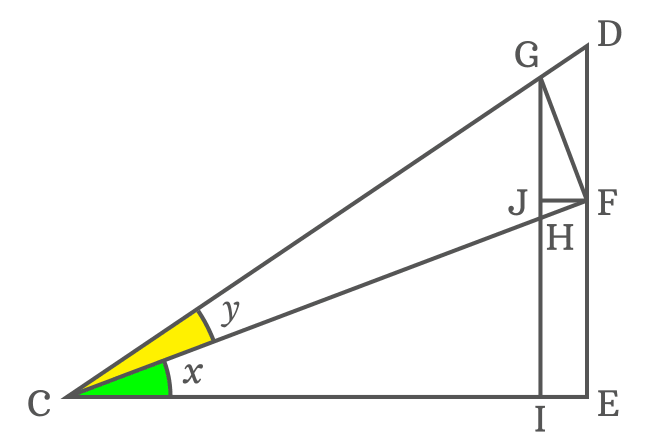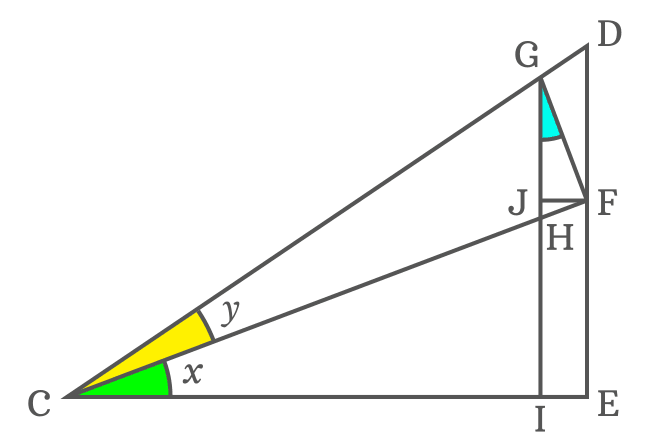
$(2). \,\,\,$ Draw a perpendicular line to side $\overline{CF}$ towards side $\overline{CD}$ and it cuts the side $\overline{CD}$ at point $G$. Therefore, $CF \perp GF$.
$(3). \,\,\,$ Draw a perpendicular line to side $\overline{CE}$ from point $G$. It intersects the side $\overline{CF}$ at point $H$ and also perpendicularly intersects the side $\overline{CE}$ at point $I$.
$(4). \,\,\,$ Now, draw a perpendicular line to side $\overline{GI}$ from point $F$ and it cuts the side $\overline{GI}$ at point $J$.
The $\Delta ECF$ with angle $x$, $\Delta FCG$ with angle $y$ and another right triangle ($\Delta JGF$) with unknown angle are formed geometrically by the above steps.
Let’s start to derive the angle sum property for the sin function in the form of $\sin{(x+y)}$ formula in trigonometry by the geometric system from the above constructed triangle.
The angle of $\Delta ICG$ is $x+y$. So, the sin of sum of two angles can be written in its ratio form from this triangle.
$\sin{(x+y)}$ $\,=\,$ $\dfrac{GI}{CG}$
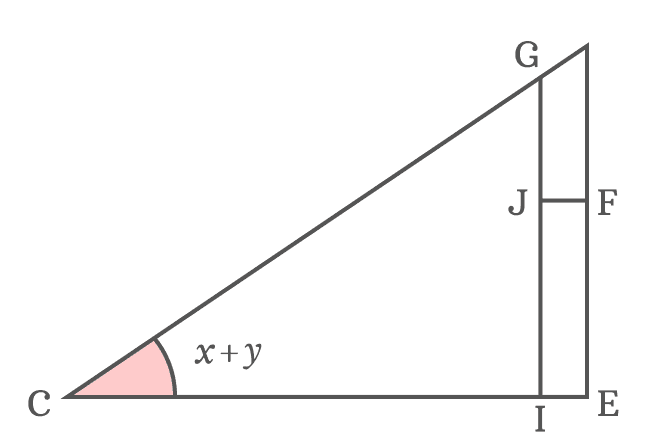
The side $\overline{JF}$ divides the side $\overline{GI}$ as two sides $\overline{GJ}$ and $\overline{JI}$. Therefore, $GI \,=\, GJ+JI$. Now, substitute $GI$ by its equivalent value in the expansion of $\sin{(x+y)}$.
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\dfrac{GJ+JI}{CG}$
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\dfrac{GJ}{CG}+\dfrac{JI}{CG}$
The sides $\overline{JI}$ and $\overline{EF}$ are parallel lines and they are equal geometrically. It means $JI = EF$.
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\dfrac{GJ}{CG}+\dfrac{EF}{CG}$
$GJ$ is length of the side and it cannot be written in terms of trigonometric functions due to unknown angle of the $\Delta JGF$. Let’s first find the $\angle JGF$ and then express $GJ$ in the form a trigonometric function.
$\angle JFC$ and $\angle ECF$ are alternate interior angles, formed by the parallel lines $\overline{JF}$ and $\overline{CE}$, and their transversal $\overline{CF}$. The alternate interior angles are equal geometrically.
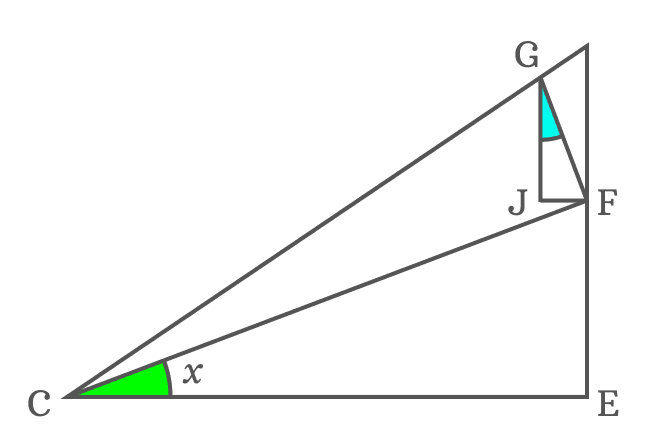
$\angle JFC \,=\, \angle ECF$
Actually, $\angle ECF = x$
$\therefore \,\,\,\,\,\, \angle JFC \,=\, x$
It is taken that $\overline{GF} \perp \overline{CF}$. So, $\angle CFG = 90^°$. The side $\overline{JF}$ divides the $\angle CFG$ as two angles $\angle CFJ$ and $\angle JFG$.
$\angle CFG \,=\, \angle CFJ + \angle JFG$
$\implies 90^° = x+\angle JFG$
$\,\,\, \therefore \,\,\,\,\,\, \angle JFG = 90^°-x$
In $\Delta JGF$, the $\angle GJF$ is $90^°$ and $\angle JFG$ is calculated as $90^°-x$. The $\angle JGF$ can be evaluated by them by using sum of angles of a triangle rule.
$\angle JGF + \angle GFJ + \angle FJG$ $\,=\,$ $180^°$
$\implies$ $\angle JGF + 90^°-x + 90^°$ $\,=\,$ $180^°$
$\implies$ $\angle JGF + 180^°-x$ $\,=\,$ $180^°$
$\implies$ $\angle JGF$ $\,=\,$ $180^°-180^°+x$
$\implies$ $\angle JGF$ $\,=\,$ $\require{cancel} \cancel{180^°}-\cancel{180^°}+x$
$\,\,\, \therefore \,\,\,\,\,\,$ $\angle JGF \,=\, x$
It is proved that the $\angle JGF$ is $x$ but the $\angle ECF$ is also $x$. It proves that $\angle ECF$ and $\angle JGF$ are similar triangles.
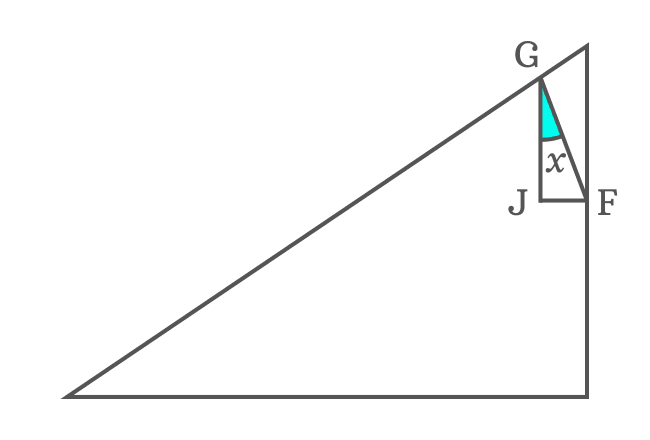
According to $\Delta JFG$, try to write the length of side $\overline{GJ}$ in terms of a trigonometric function.
$\cos{x} \,=\, \dfrac{GJ}{GF}$
$\implies GJ = {GF}\cos{x}$
Now, substitute the equivalent value of $GJ$ in the expansion of sin of sum of two angles function.
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\dfrac{{GF}\cos{x}}{CG}$ $+$ $\dfrac{EF}{CG}$
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\dfrac{GF}{CG} \, \cos{x}$ $+$ $\dfrac{EF}{CG}$
According to $\Delta FCG$, the $GF$ and $CG$ are lengths of the sides $\overline{GF}$ and $\overline{CG}$ respectively. The ratio between them can be represented by a sin function.
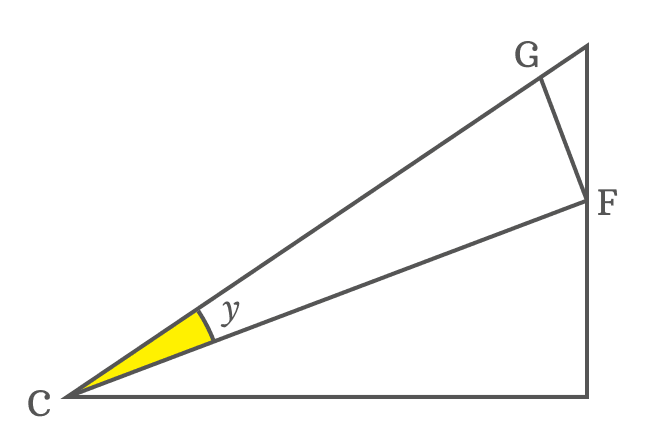
$\sin{y} \,=\, \dfrac{GF}{CG}$
The ratio of $GF$ to $CG$ can be replaced by $\sin{y}$ function in the expansion of sin of sum of angles $x$ and $y$.
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\sin{y}\cos{x}$ $+$ $\dfrac{EF}{CG}$
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\cos{x}\sin{y}$ $+$ $\dfrac{EF}{CG}$
The first term in the expansion of $\sin{(x+y)}$ function is successfully expressed in the form of trigonometric functions. Similarly, let’s try to transform the second term.
$EF$ is side of $\Delta ECF$. According to this right triangle, the length of the side $\overline{EF}$ can be written in trigonometric function form.
$\sin{x} \,=\, \dfrac{EF}{CF}$
$\implies EF = {CF}\sin{x}$
The length of the side $\overline{EF}$ can be replaced by its equivalent value in the expansion of sin of compound angle function.
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\cos{x}\sin{y}$ $+$ $\dfrac{{CF}\sin{x}}{CG}$
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\cos{x}\sin{y}$ $+$ $\dfrac{CF}{CG} \, \sin{x}$
There is only one ratio between two sides left in the expansion of sin of compound angle function. The $CF$ and $CG$ are lengths of the sides $\overline{CF}$ and $\overline{CG}$ and they are part the $\Delta FCG$.

According to $\Delta FCG$
$\cos{y} \,=\, \dfrac{CF}{CG}$
The ratio of $CF$ to $CG$ can be replaced by its trigonometric function in the expansion of sin of sum of two angles $x$ and $y$.
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\cos{x}\sin{y}$ $+$ $\cos{y}\sin{x}$
$\implies$ $\sin{(x+y)}$ $\,=\,$ $\cos{x}\sin{y}$ $+$ $\sin{x}\cos{y}$
$\,\,\, \therefore \,\,\,\,\,\,$ $\sin{(x+y)}$ $\,=\,$ $\sin{x}\cos{y}$ $+$ $\cos{x}\sin{y}$
It is proved that the sin of sum of two angles is expanded as the sum of the products of sin and cos of angles. It is called as the angle sum identity for sin function and it is used as a trigonometric formula to expand sin function which contains sum of two angles as angle.
The sin of sum of two angles formula is written in several ways but there are three standard forms.
If you take angles $A$ and $B$ instead of $x$ and $y$, then the angle sum property in the form of sin function is proved as follows.
$\sin{(A+B)}$ $\,=\,$ $\sin{A}\cos{B}$ $+$ $\cos{A}\sin{B}$
Similarly, if you take $\alpha$ and $\beta$ as angles instead of $x$ and $y$, then the angle sum identity is proved as follows.
$\sin{(\alpha+\beta)}$ $\,=\,$ $\sin{\alpha}\cos{\beta}$ $+$ $\cos{\alpha}\sin{\beta}$
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved