The value of sine function for angle $60$ degrees is called sine of angle $60$ degrees. It is represented as $\sin{60^\circ}$ or $\sin{\Big(\dfrac{\pi}{3}\Big)}$ generally in trigonometric mathematics.
$\sin{60^\circ} \,=\, \dfrac{\sqrt{3}}{2}$
The exact value of $\sin{60^\circ}$ is in fraction and $0.866$ in decimal form. The value of sine of angle $60$ degrees can be evaluated in two geometrical methods.
It is a geometrical method, which is used to derive the value of sin $60$ degrees in fraction form and it is actually done on the basis of a special geometrical relation between opposite side and hypotenuse when the angle of the triangle is $60^\circ$ or $\dfrac{\pi}{3}$.
The geometrical property between them discloses that the length of opposite side is exactly equal to the $\dfrac{\sqrt{3}}{2}$ times to the length of the hypotenuse.
$Length \, of \, Opposite \, side$ $\,=\,$ $\dfrac{\sqrt{3}}{2}$ $\times$ $Length \, of \, Hypotenuse$
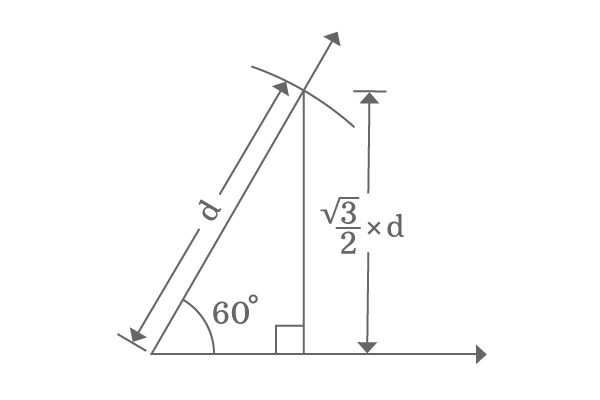
$\implies$ $\dfrac{Length \, of \, Opposite \, side}{Length \, of \, Hypotenuse}$ $\,=\,$ $\dfrac{\sqrt{3}}{2}$
According to trigonometry, the ratio of length of the opposite side to length of hypotenuse is called sine but this ratio is calculated at $60$ degrees angle. So, the ratio of lengths of opposite side to hypotenuse can be expressed as $\sin{60^\circ}$ in mathematics.
$\,\,\, \therefore \,\,\,\,\,\,$ $\sin{60^\circ} \,=\, \dfrac{\sqrt{3}}{2}$
Thus, the value of sine $60$ degrees is calculated exactly as $\dfrac{\sqrt{3}}{2}$ in fraction from theoretically in geometrical method.
$\sin{60^\circ} \,=\, \dfrac{\sqrt{3}}{2} \,\approx\, 0.866$
The value of $\sin{\Big(\dfrac{\pi}{3}\Big)}$ is $0.866$ approximately.
The value of $\sin{60^\circ}$ can be calculated in geometrical method practically by constructing a right angled triangle with an angle $60$ degrees.
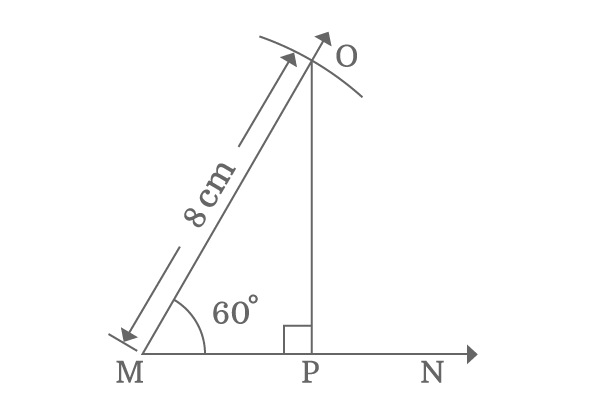
Firstly, draw a horizontal ray $\overrightarrow{MN}$ by the ruler and then draw a $60$ degrees line in anticlockwise direction from point $M$ by the protractor.
Later, take compass and adjust it to any length (in this case $8 \, cm$) with the help of a ruler and then draw an arc from point $M$ on $60$ degrees line and it intersects the $60$ degrees line at point $O$.
Finally, draw a perpendicular line to horizontal ray from point $O$ to complete the construction of a right angled triangle ($\Delta PMO$).
The angle of the right angled triangle $PMO$ is $60^\circ$. So, evaluate the sin $60$ degrees by calculating the ratio of length of opposite side ($OP$) to length of hypotenuse ($OM$).
$\sin{60^\circ} \,=\, \dfrac{OP}{OM}$
In this case, the length of the hypotenuse is taken as $8 \, cm$ but the length of the opposite side is unknown. However, it can be measured by the ruler. You will observe that the length of the opposite side ($OP$) lies between $6.9 \, cm$ and $7 \, cm$. Just take it as $6.95 \, cm$.
$\implies \sin{60^\circ} \,=\, \dfrac{6.95}{8}$
$\,\,\, \therefore \,\,\,\,\,\, \sin{60^\circ} \,=\, 0.86875$
The value of $\sin{60^\circ}$ is $0.86875$ practically but it changes every time because it depends on the measurement of length of opposite side but the values which are determined in practical geometrical method are very closer to $0.866$ all the time.
The only reason behind for this is $\dfrac{\sqrt{3}}{2}$ (or) $0.866$ is the exact value of sin function for angle $60^\circ$.
A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.
Copyright © 2012 - 2025 Math Doubts, All Rights Reserved