Properties of sides of Right angled triangle when angle is 60°

Properties

There are two fundamental relations between sides of a right triangle when its angle equals to $60$ degrees.

1. The length of adjacent side is equal to half of the length of hypotenuse.
2. The length of opposite side is equal to $\small \sqrt{3}/{2}$ times of the length of hypotenuse.
3. The third angle of right triangle is $\small 30^°$.

Theorem

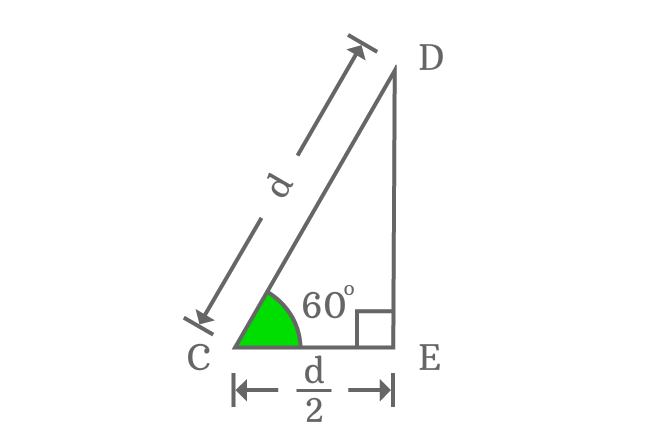
Draw a horizontal straight line $\overrightarrow{ST}$, and then draw a $60$ degrees line from point $S$ in anticlockwise direction. Set compass to any length with the help of a ruler and then draw an arc on $60$ degree line from $S$ and their intersecting point is $U$. After that, use protractor and draw a perpendicular line to straight line $\overrightarrow{ST}$ from point $U$ and take, it intersects the straight line $\overrightarrow{ST}$ at point $V$. Thus a right angled triangle $VSU$ is formed with an angle of $60^\circ$.

Result

Take, the length of the side $\overrightarrow{SU}$ is $d$. but the length of the adjacent side $\overline{SV}$ will be $\dfrac{d}{2}$. Now, evaluate the length of the opposite side $\overline{UV}$ and it can be done by using Pythagorean Theorem.

${SU}^2 \,=\, {SV}^2 + {UV}^2$

$\implies UV \,=\, \sqrt{{SU}^2 -{SV}^2}$

$\implies UV \,=\, \sqrt{d^2 -{\Bigg(\dfrac{d}{2}\Bigg)}^2}$

$\implies UV \,=\, \sqrt{d^2 -\dfrac{d^2}{4}}$

$\implies UV \,=\, \sqrt{\dfrac{4d^2 -d^2}{4}}$

$\implies UV \,=\, \sqrt{\dfrac{3d^2}{4}}$

$\implies UV \,=\, \dfrac{\sqrt{3}d}{2}$

$\,\,\, \therefore \,\,\,\,\,\, UV \,=\, \dfrac{\sqrt{3}}{2} \times {SU}$

Proof

The two properties of the sides of right angled triangle can be proved practically when the angle of right angled triangle is $60^\circ$.

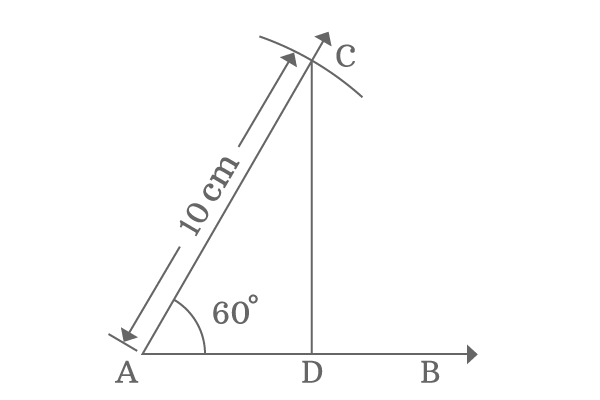
Draw a horizontal ray $\overrightarrow{AB}$ and then draw a $60$ degrees line in anticlockwise direction from point $A$. After that, set compass to any length with the help of a ruler. In this case, compass is set to $10 \, cm$ and draw an arc on $60^\circ$ line from point $A$ and their intersecting point is $C$.

Finally, draw a perpendicular line to ray $\overrightarrow{AB}$ from point $C$ and it intersects the ray $\overrightarrow{AB}$ at point $D$. Thus, a right angled triangle, called $\Delta DAC$ is formed geometrically.

Take ruler and check the length of adjacent side ($\overline{AD}$) and you observe that it will be $5 \, cm$ exactly. It is proved that the length of adjacent side is exactly half of the length of the hypotenuse of right angled triangle when the angle of triangle is $60^\circ$.

Now, take ruler and measure the length of the opposite side $\overline{CD}$. You will observe that it will be more than $8.65 \, cm$ but very close to $8.7 \, cm$.

Theoretically, the value of opposite side is $\dfrac{\sqrt{3}}{2} \times 10 \,=\, 8.6602$

Hence, the length of the opposite side is more than $8.65 \, cm$ but less than $8.7 \, cm$.

Therefore, it is proved that the length of opposite is $\dfrac{\sqrt{3}}{2}$ times to length of hypotenuse when the angle is equal to $60^\circ$.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.