Similar Triangles

The triangles that have equal corresponding angles and proportional corresponding sides are called similar triangles.

Introduction

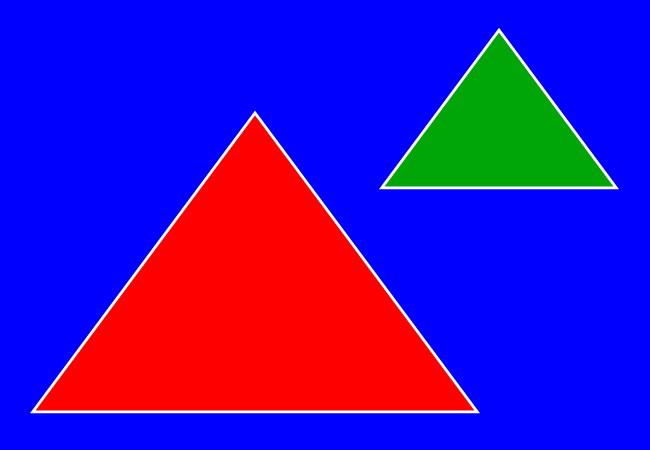
The similarity of any two triangles is determined by verifying the following two geometrical aspects.

1. The equality of corresponding angles of the triangles.
2. The proportionality of corresponding sides of the triangles.

When any two triangles have the same properties, then one triangle is similar to another triangle and vice-versa. The two triangles are simply called the similar triangles.

Example

$\Delta LMN$ and $\Delta PQR$ are two triangles. Now, let’s check the similarity of both triangles.

Angles

In $\Delta LMN$, the interior angles are $\angle NLM$, $\angle LMN$ and $\angle MNL$. The three angles of $\Delta PQR$ are $\angle RPQ$, $\angle PQR$ and $\angle QRP$.

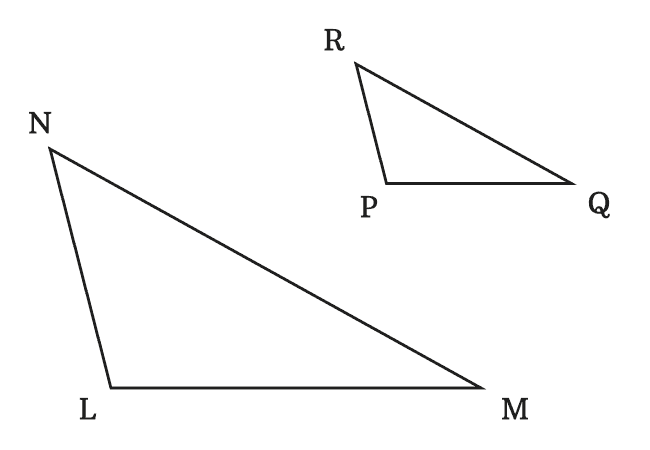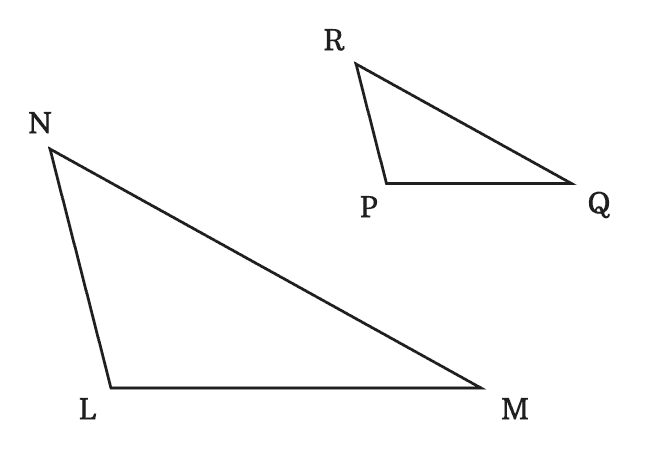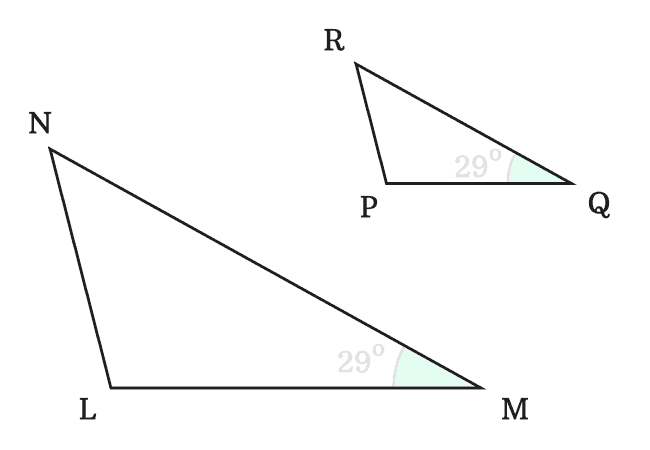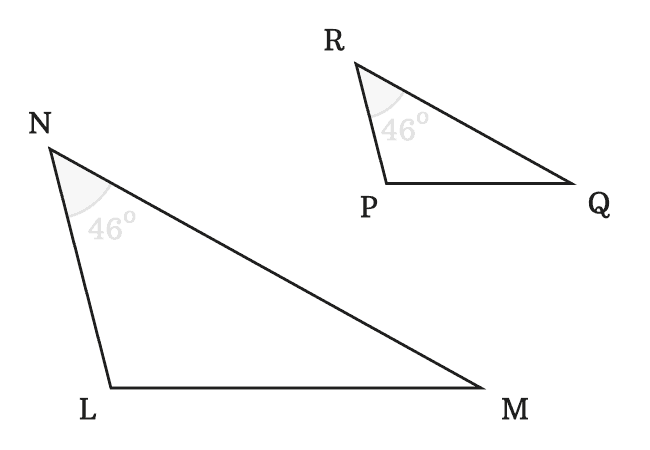
The corresponding angles of $\angle NLM$, $\angle LMN$ and $\angle MNL$ are $\angle RPQ$, $\angle PQR$ and $\angle QRP$ respectively. Now, measure three angles of both triangle by a protractor and then compare them one by one.

$(1).\,\,\,$ $\angle NLM \,=\, \angle RPQ \,=\, 105^°$

$(2).\,\,\,$ $\angle LMN \,=\, \angle PQR \,=\, 29^°$

$(3).\,\,\,$ $\angle MNL \,=\, \angle QRP \,=\, 46^°$

The comparison of corresponding angles of triangles has cleared that the corresponding angles of the two triangles $LMN$ and $PQR$ are equal.

Sides

In $\Delta LMN$, the sides are $\overline{LM}$, $\overline{MN}$ and $\overline{NL}$. Similarly, $\overline{PQ}$, $\overline{QR}$ and $\overline{RP}$ are three sides of the $\Delta PQR$. In this example, the corresponding side of $\overline{LM}$ is $\overline{PQ}$, the corresponding side of $\overline{MN}$ is $\overline{QR}$ and the corresponding side of $\overline{NL}$ is $\overline{RP}$. Now, measure the length of each side of every triangle by a ruler. Later, compare lengths of their corresponding sides.

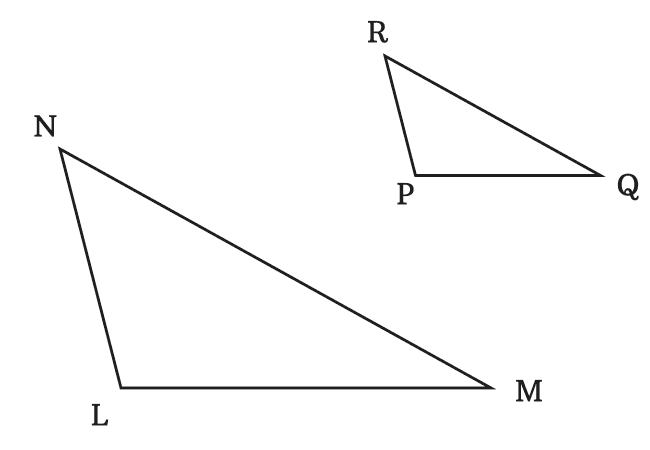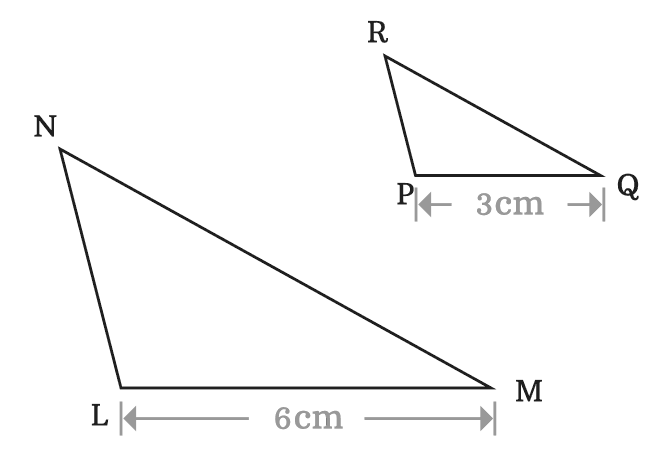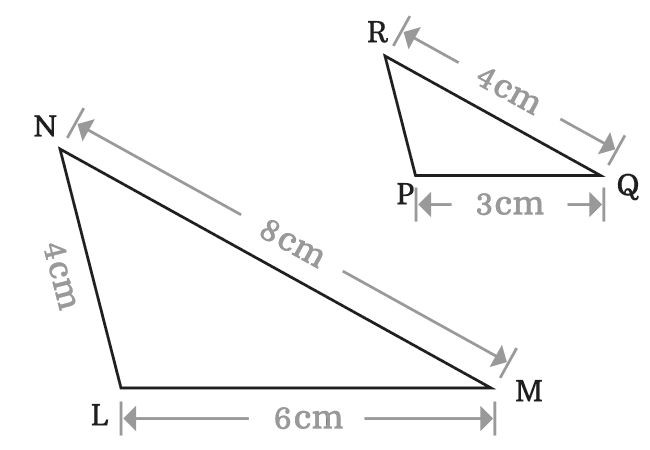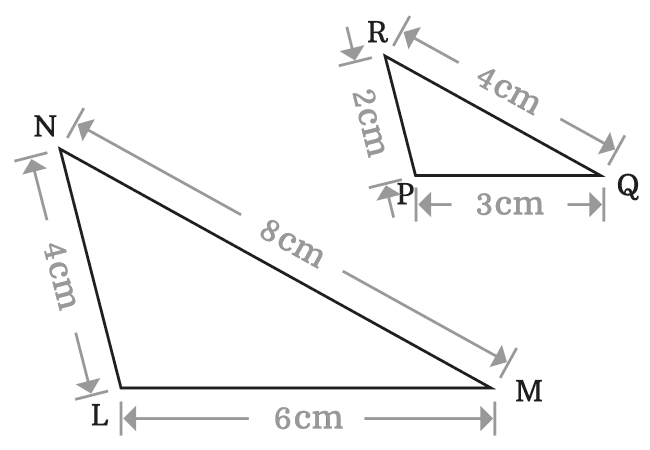
$(1).\,\,\,$ $LM \,=\, 6\,cm$ and $PQ \,=\, 3\,cm$

$\implies$ $LM \,=\, 2 \times PQ$

The corresponding sides $\overline{LM}$ and $\overline{PQ}$ are proportional.

$(2).\,\,\,$ $MN \,=\, 8\,cm$ and $QR \,=\, 4\,cm$

$\implies$ $MN \,=\, 2 \times QR$

The corresponding sides $\overline{MN}$ and $\overline{QR}$ are proportional.

$(3).\,\,\,$ $NL \,=\, 4\,cm$ and $RP \,=\, 2\,cm$

$\implies$ $NL \,=\, 2 \times RP$

The corresponding sides $\overline{NL}$ and $\overline{RP}$ are proportional.

According to the comparison of corresponding sides of both triangles, the corresponding sides of both triangles are proportional.

Due to the equality of corresponding angles and proportionality of corresponding sides, the $\Delta LMN$ and $\Delta PQR$ are called similar triangles.

Representation

The similarity of the triangles is written mathematically in a special way.

1. The triangle $LMN$ is similar to the triangle $PQR$ and it is written as $\Delta LMN \sim \Delta PQR$ mathematically.
2. Similarly, the triangle $PQR$ is similar to the triangle $LMN$, and it is expressed as $\Delta PQR \sim \Delta LMN$ in mathematics.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.