Sign of Tan function in first quadrant

Sign

$\sin{\theta} \, > \, 0$

The sign of tan function in first quadrant of two-dimensional space is positive.

Proof

The sign of tan function in first quadrant of two-dimensional Cartesian coordinate system can be proved geometrically. It helps us to understand how the sign of tangent function in first quadrant is positive.

1. Let $E$ be a point in first quadrant of two-dimensional Cartesian coordinate system.
2. Connect the point $E$ with the origin of two-dimensional space by a line.
3. Draw a perpendicular line to horizontal axis from point $E$ and it intersects the $x$-axis at point $F$.

Thus, a right triangle is constructed geometrically and let’s take the angle of $\Delta EOF$ as theta ($\theta$). Therefore, the tangent function is written as $\tan{\theta}$ in trigonometry.

Let’s take the length of adjacent side is denoted by $x$ and the length of opposite side is represented by $y$. Now, express the tan function in ratio form of lengths of sides.

$\tan{\theta} \,=\, \dfrac{EF}{OF}$

In this case, $EF = y$ and $OF = x$.

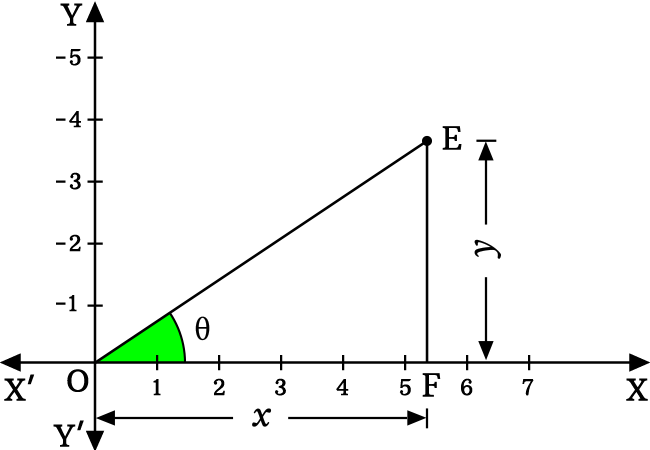
$\implies \tan{\theta} \,=\, \dfrac{y}{x}$

In this case, the variable $x$ represents any value on the $x$-axis. Similarly, the variable $y$ represents any value on the $y$-axis. Actually, the $x$-axis and $y$-axis both represent positive values in first quadrant. Therefore, the lengths of opposite and adjacent sides should be positive. Therefore, $x > 0$ and $y > 0$.

$\implies \tan{\theta} \,=\, \dfrac{y}{x}$

In first quadrant, the values of $x$ and $y$ are positive. So, the quotient of them should also be positive. Therefore, the sign of tan function value is also positive.

$\,\,\, \therefore \,\,\,\,\,\, \tan{\theta} \, > \, 0$

Example

$\Delta POQ$ is a right triangle in first quadrant of two dimensional space. The angle of this triangle is $\alpha$. The tangent function can be expressed in ratio form of lengths of sides.

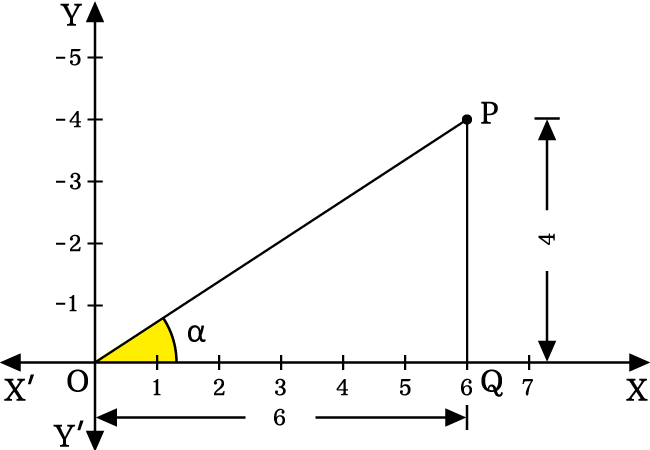
$\tan{\alpha} \,=\, \dfrac{PQ}{OQ}$

In this example, $PQ \,=\, 4$ and $OQ \,=\, 6$. The sign of length of each side is positive. Now, substitute the lengths of sides in the ratio for calculating the tan value.

$\implies \,\,\,$ $\tan{\alpha} \,=\, \dfrac{4}{6}$

$\require{cancel} \implies \,\,\,$ $\tan{\alpha} \,=\, \dfrac{\cancel{4}}{\cancel{6}}$

$\implies \,\,\,$ $\tan{\alpha} \,=\, \dfrac{2}{3}$

The value of tan function $\tan{\alpha}$ is positive and it can be understood that the sign of tan function in first quadrant is positive.

A free math education service for students to learn every math concept easily, for teachers to teach mathematics understandably and for mathematicians to share their maths researching projects.